一道应用回归与卡尔曼滤波进行预测的小题目

发表于 | 分类于 | 浏览 次

一道应用回归与卡尔曼滤波进行预测的小题目

今天Po一道题目的解决方法，是月同小仙女问的我关于熊老师《交通数据采集与处理》课程的内容，感觉一言两语说不清楚，于是决定写下来手动帮助一下快要期末考的小伙伴。

题目要求

题1：假设某地统计过去五个月的气温与出行量之间的关系如下：

月份： 1 2 3 4 5
气温(℃)： 10 15 14 20 22
出行量(千人次)： 21 32 34 41 60

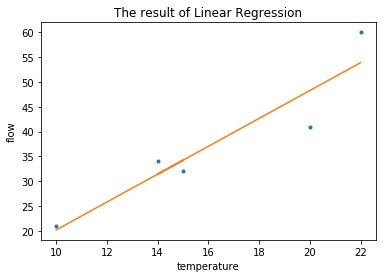
同时预计6月气温为24度，请用一次线性回归预测6月出行量。

题2：请用二次线性回归预测6月出行量

题3：请用卡尔曼滤波预测6月出行量(提示：不足的条件自行合理假设)

题4：上述那个预测结果比较好？“好”的定义是什么？

题5：开放性问题，是否能设想比上述模型更好的模型？

问题一：线性回归

关于线性回归的部分解释和推导，可以参考我的博客：[线性回归的解释]https://qianni1997.github.io/2018/05/28/ML-regression/

其实在线性回归$Y=X\omega$中我们的目的就是最小化误差平方和即：

经过一起系列推导，我们可以得知，实现上式最小化时，线性回归的系数估计结果为：

因此我们在此问中的工作就是构造$X​$,$Y​$，并利用上式求解得到$\hat\omega​$

提前阐述的概念

  • 本问题中，输入：气温数据；输出：出行量。
  • 我们将数据集中的样本个数记为m，特征个数记为n（本问题中我们有5个月份的气温数据，因此m=5;因为用于输入的特征仅有气温，所以此处记n=1）

构造Y

Y是线性回归的结果，即输出（出行量），我们将Y构造为$m*1$阶矩阵

1
2
import numpy as np
Y = np.array([[21],[32],[34],[41],[60]])
1
Y
array([[21],
       [32],
       [34],
       [41],
       [60]])

构造X

X是线性回归的输入，因为回归中存在常数项，因此我们除了气温这一列以外，在前面补充一列全1的列。因此此时我们的输入X是一个$5*2$阶的矩阵

1
X_1d = np.array([[1,1,1,1,1],[10,15,14,20,22]])
1
2
X_1d = X_1d.T
X_1d
array([[ 1, 10],
       [ 1, 15],
       [ 1, 14],
       [ 1, 20],
       [ 1, 22]])

$\hat\omega$的计算

1
w_hat = np.dot(np.linalg.inv(np.dot(X_1d.T,X_1d)),np.dot(X_1d.T,Y))#执行w的估计公式
1
w_hat
array([[-7.85775862],
       [ 2.80603448]])

6月出行量的预测与误差平方和计算

以上就是我们计算得到的线性回归的系数$\hat\omega$

接下来，我们用这个回归系数，预测6月份的出行量

1
2
x_1d_6 = np.array([[1,24]])
np.dot(x_1d_6,w_hat)#一次线性回归预测得到的6月的出行量
array([[ 59.48706897]])

我们也可以计算一下，一次线性回归的误差平方和是多少：

1
2
error_1d = np.dot((Y-np.dot(X_1d,w_hat)).T,(Y-np.dot(X_1d,w_hat)))
error_1d
array([[ 102.50862069]])

1
2
3
4
5
6
7
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(X_1d[:,1],Y, ".")
plt.plot(X_1d[:,1],np.dot(X_1d,w_hat))
plt.xlabel('temperature')
plt.ylabel('flow')
plt.title('The result of Linear Regression');

png

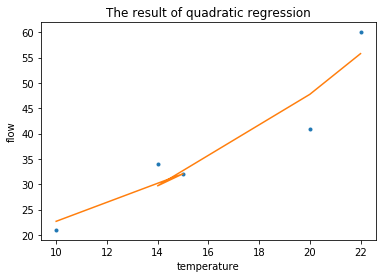
问题二：二次回归

二次回归与以上线性回归的理论相同，只是在X的构造方面有所区别

构造X

在二次回归中，我们不仅仅需要输入常数项（之前提及的全1列）、气温，还需要输入气温的平方。这样做相当于把一个二次的问题转化为了线性的问题，从而可以用之前的理论进行求解,现在，我们的X为一个$5*3$阶的输入

1
2
3
X_2d = np.array([[1,1,1,1,1],[10,15,14,20,22],[10*10,15*15,14*14,20*20,22*22]])
X_2d = X_2d.T
X_2d
array([[  1,  10, 100],
       [  1,  15, 225],
       [  1,  14, 196],
       [  1,  20, 400],
       [  1,  22, 484]])

接下来的求解、预测、计算步骤

1
2
w_hat_2d = np.dot(np.linalg.inv(np.dot(X_2d.T,X_2d)),np.dot(X_2d.T,Y))#执行w的估计公式
w_hat_2d
array([[ 22.817038  ],
       [ -1.2703054 ],
       [  0.12584309]])

1
2
x_2d_6 = np.array([[1,24,24*24]])
np.dot(x_2d_6,w_hat_2d)#二次回归预测得到的6月的出行量
array([[ 64.81533066]])

1
2
error_2d = np.dot((Y-np.dot(X_2d,w_hat_2d)).T,(Y-np.dot(X_2d,w_hat_2d)))
error_2d
array([[ 84.75715044]])

1
2
3
4
5
plt.plot(X_2d[:,1],Y, ".")
plt.plot(X_2d[:,1],np.dot(X_2d,w_hat_2d))
plt.xlabel('temperature')
plt.ylabel('flow')
plt.title('The result of quadratic regression');

png

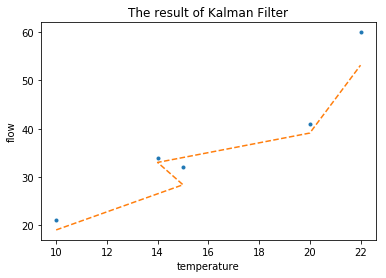
问题三：Kalman Filter

卡尔曼滤波是用于状态估计、预测的较为经典的理论，我们在不同的课上已经接触过N多遍，只是由于一直没有去手动实现一下，所以理解的并不太清晰。以及由于公式中涉及到高斯分布均值呀方差呀的参数，每个老师都会用不同的符号去表示，有时也会省略一部分参数，导致每一次学都感觉像是一个全新的理论。。

  • 由于我们在日常生活中会用模型与实测数据两种方式去刻画某一个量，但这两种方式都不准确，因此卡尔曼滤波能够融合这两种方式，以更好地估计某一个量。
  • Kalman Filter核心是：预测与更新两个步骤；预测步骤基于模型(状态演化过程计算式)，更新步骤基于实测数据

理论部分我就不再具体阐述了，可以参考以下链接文章：

[推荐一个较为生动形象的理论讲解文章]http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/

文章中的结论为：
预测过程

更新过程

其中：

更新过程修正一下

其中：

Kalman filter函数的定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def predict(posterior,movement):
    x,P = posterior
    dx,Q = movement
    x = x + dx
    P = P + Q
    return x,P
def update(prior,measurement):
    x,P = prior
    z,R = measurement
    K = P / (P + R)
    y = z - x
    x = x + K*y
    P = (1 - K)*P
    return x,P
1
2
3
4
5
6
7
8
9
10
11
12
def kalman_filter(Y, x0=10, P=1, dx=3, Q=1, R=1):
    result = []
    posterior = (x0, P)
    movement = (dx, Q)
    for y in Y:
        measurement = (y, R)
        aprior = predict(posterior, movement)
        print(aprior)
        posterior =  update(aprior, measurement)
        print(posterior, "--")
        result.append(posterior)
    return result

使用Kalman滤波

1
r1 = kalman_filter(Y, Q=0.5, R=0.5);
(13, 1.5)
(array([ 19.]), 0.375) --
(array([ 22.]), 0.875)
(array([ 28.36363636]), 0.3181818181818182) --
(array([ 31.36363636]), 0.8181818181818181)
(array([ 33.]), 0.31034482758620685) --
(array([ 36.]), 0.8103448275862069)
(array([ 39.09210526]), 0.30921052631578944) --
(array([ 42.09210526]), 0.8092105263157894)
(array([ 53.16080402]), 0.3090452261306532) --

1
2
3
4
5
6
7
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(X_1d[:,1],Y, ".")
plt.plot(X_1d[:,1],[r[0] for r in r1], "--")
plt.xlabel('temperature')
plt.ylabel('flow')
plt.title('The result of Kalman Filter');

png

进行预测

1
2
3
4
5
6
7
8
9
10
11
dx=3
q=0.5
r=0.5
x_6=r1[-1][0][0]+dx#x = x + dx
print('predict June:',x_6)
p_6=r1[-1][1]+q#P = P + Q
k_6=p_6/(p_6+r) 
z=62#估计六月观测为62
y=z-x_6#z
x_6=x_6+k_6*y
print('update June:',x_6)
predict June: 56.1608040201
update June: 59.7696737044

PS:感觉用Kalman Filter做这个题有点儿迷，我其实并不太确定是不是这样，因为我并没有使用温度数据，且很多参数都是我假设的

剩下的4.5两题比较开放，“好”个人理解需要选择评判指标，比如很多都是在最小化误差平方和，当然也可以选择一些其他的。

至于其他的预测方法，我想到的譬如《预测与决策方法》课上的滑动平均、指数平滑，建模里面的ARIMA模型等等吧。

希望能给大家一点点小启发~