机器学习之聚类算法

机器学习之聚类算法(1)

1. 聚类的概念(Clustering)

1.1 聚类的概念

机器学习按照学习形式可以分为“监督学习”与“无监督学习”，在无监督学习中，训练样本的标记信息未知，即没有“标签”，需要通过对无标记训练样本的学习来揭示数据的内在性质与规律，无监督学习任务中研究最多、应用最广的是聚类。

聚类将数据集中相似的样本归到同一个簇中，将不相似的地样本归到不同的簇中，每个簇可能对应于一些潜在的概念（类别），但这些概念对聚类算法而言事先是未知的。这其中的一系列概念可以表示为：

假定样本集$D=\left\{x_1,x_2,\cdots,x_m \right\}$包含$m$个无标记样本，每个样本$x_i=\left\{x_{i1};x_{i2};\cdots;x_{in} \right\}$是一个$n$维特征向量，则聚类算法将样本集$D$划分为$k$个不相交的簇$\left\{C_l | l=1,2,\cdots,k \right\}$,其中，$C_{l’}\cap_{l’\neq l}C_l=\varnothing $且$D=\cup_{l=1}^kC_l$，相应地，我们用$\lambda_j\in\left\{1,2,\cdots,k\right\}$表示样本$x_j$的簇标记，即$x_j\in C_{\lambda_j}$于是，聚类的结果可用包含$m$个元素的簇标记向量$\lambda=\left(\lambda_1;\lambda_2; \cdots;\lambda_m\right)$表示。

1.2 聚类中的性能度量

聚类分析试图将相似对象划为同一簇，不相似的对象归到不同簇，而“相似”主要依靠性能度量。

聚类的性能度量（有效性指标）是用于评估聚类效果的好坏的或作为聚类过程的优化目标的。聚类性能度量大致可以分为两类，一类是将聚类结果与某个“参考模型”进行比较，称为“外部指标”；另一类是直接考察聚类结果而不利用任何参考模型，称为“内部指标”。

1.2.1 外部指标

对数据集$D=\left\{x_1,x_2,\cdots,x_m \right\}$，假定通过聚类给出的簇划分为$C=\left\{C_1,C_2,\cdots,C_k \right\}$参考模型给出的簇划分为$C^=\left\{C_1^,C_2^,\cdots,C_s ^\right\}$。相应地，令$\lambda$与$\lambda^$分别表示$C$与$C^$对应的簇标记向量，将样本两两配对考虑，则可定义：

$$a=\left|SS\right|, SS=\left\{(x_i,x_j)|\lambda_i=\lambda_j,\lambda_i^*=\lambda_j^*,i<j\right\}$$ $$b=\left|SD\right|, SD=\left\{(x_i,x_j)|\lambda_i=\lambda_j,\lambda_i^*\neq\lambda_j^*,i<j\right\}$$ $$c=\left|DS\right|,DS=\left\{(x_i,x_j)|\lambda_i\neq\lambda_j,\lambda_i^*=\lambda_j^*,i<j\right\}$$ $$d=\left|DD\right|, SS=\left\{(x_i,x_j)|\lambda_i\neq\lambda_j,\lambda_i^*\neq\lambda_j^*,i<j\right\}$$

其中集合$SS$为在$C$中隶属于相同簇且在$C^*$中也隶属于相同簇的样本对，其余同理可以推得，此外$a+b+c+d=\frac{m(m-1)}{2}$

通过以上定义得到聚类性能度量的外部指标：

• Jaccard系数 $JC=\frac{a}{a+b+c}$
• FM指数 $FMI=\sqrt{\frac{a}{a+b}\frac{a}{a+c}}$
• Rand指数 $RI=\frac{2(a+d)}{m(m-1)}$

1.2.2 内部指标

根据簇划分$C=\left\{C_1,C_2,\cdots,C_k \right\}$，定义：

$$avg(C)=\frac{2}{\left|C\right|(\left|C\right| - 1)}\sum_{1\leq i<j\leq\left|C\right|}dist(x_i,x_j)$$ $$diam(C)=\max_{1\leq i<j\leq\left|C\right|}dist(x_i,x_j)$$ $$d_\min (C_i,C_j)=\min_{x_i\in C_i,x_j \in C_j}dist(x_i,x_j)$$ $$d_{cen}(C_i,C_j)=dist(\mu_i,\mu_j)$$

$dist$为样本距离计算公式，$\mu$代表簇$C$的中心点，$avf(C)$对应簇$C$内样本间的平均距离，$diam(C)$对应簇内$C$内样本间的最远距离，$d_\min (C_i,C_j)$为两个簇最近样本间的距离$d_{cen}(C_i,C_j)$为两簇中心点间的距离。

通过以上可以导出以下内部指标：

• DBI指数 $DBI =\frac{1}{k}\sum_{i=1}^k\max_{j\neq i}\left( \frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu_i,\mu_j)}\right)$
• Dunn指数 $DI=\min_{1\leq i \leq k}\left\{\min_{j\neq i}\left(\frac{d_\min(C_i,C_j)}{\max_{1\leq l \leq k}diam(C_l)}\right)\right\}$

DBI的值越小越好，DI的值越大越好。

1.3 聚类中的距离

性能度量中的内部指标涉及到“距离”的度量，数据的属性可以分为“有序属性”（如{1,2,3}可以直接衡量出各个量之间的距离）与“无序属性”（如{飞机，火车，轮船}不能直接刻画各个量之间的距离）。

其中“有序属性”可以通过闵可夫斯基距离计算：

$$dist_{mk}(x_i,x_j)=\left(\sum_{u=1}^n \left|x_{iu}-x_{ju}\right|^p\right)^\frac{1}{p}$$

p=1时，为曼哈顿距离；p=2时为欧式距离；此外当样本空间中不同属性的重要性不同时，可以使用“加权距离”进行计算。

“无序属性”可以通过VDM(value Difference Metric)计算：

$$VDM_p(a,b)=\sum_{i=1}^k\left|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\right|^p$$

其中$m_{u,a}$表示在属性$u$上取值为$a$的样本数，$m_{u,a,i}$表示在第$i$个样本簇中在属性$u$上取值为$a$的样本数，$k$为样本簇数。

对于同时存在“有序属性”与“无序属性”的情况，可以采用混合距离定义，其中有$n_c$个有序属性，$n-n_c$个无序属性：

$$MinkovDM_p(x_i,x_j)=\left( \sum_{u=1}^n \left|x_{iu}-x_{ju}\right|^p+ \sum_{u=n_c+1}^n VDM_p(x_{iu},x_{ju})\right)^\frac{1}{p}$$

距离度量需要满足如非负性、同一性、对称性、直递性（两边之和大于第三边）等性质，但相似度度量的过程中使用的距离未必一定要满足距离度量的所有基本性质。

1.4 聚类的分类

看过几个版本的聚类的分类方法，基本是一致的，但也有一点点差异，此处选取周志华《机器学习》一书中的分类方法。

• 原型聚类：假设聚类结构能通过一组原型刻画，算法一般先对原型进行初始化，然后对原型进行迭代更新求解。代表方法包括k-means；LVQ；GMM等。
• 密度聚类：基于密度的方法的特点是不依赖于距离，而是依赖于密度，从而克服基于距离的算法只能发现“球形”聚簇的缺点。其核心思想在于只要一个区域中点的密度大于某个阈值，就把它加到与之相近的聚类中去。 通常情况，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的结果。代表方法包括DBSCAN、OPTICS，DENCLUE，WaveCluster等。
• 层次聚类：试图在不同层次对数据集进行划分，从而形成树型的聚类结构，存在“自底而上”的聚合策略，与“自顶而下”的分拆策略。在“自底向上”方案中，初始时每个数据点组成一个单独的组，在接下来的迭代中，按一定的距离度量将相互邻近的组合并成一个组，直至所有的记录组成一个分组或者满足某个条件为止。 代表方法包括：AGNES、BIRCH，CURE，CHAMELEON等。

2.原型聚类——K-均值聚类算法(K-means)

2.1 过程及算法

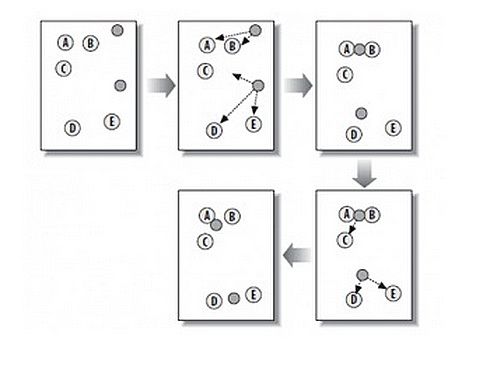
如上图所示，是K均值聚类的原理。对数据集$D=\left\{x_1,x_2,\cdots,x_m \right\}$，K-均值算法针对聚类所得簇划分$C=\left\{C_1,C_2,\cdots,C_k \right\}$最小化平方误差：

$$E=\sum_{i=1}^k \sum_{x\in C_i}\|x-\mu_i \|_2^2$$

其中k是用户给定的簇的个数，$\mu_i$是簇$C_i$的均值向量，即簇的“质心”。找到E的最小值是一个NP困难问题，k-均值算法采用贪心策略，通过迭代优化近似求解，算法首先对于质心（均值向量）进行初始化，随机确定k个初始点作为质心，然后将数据集中的每个点寻找距离其最近的质心，并将该点分给该质心代表的簇，之后更新簇的质心（均值向量）为该簇现有所有点的平均值。

伪代码过程为：

创建k个点作为起始质心（可以在样本中随机选择k个）
当任意一个点的簇分配结果发生改变时
	对数据集中的每个数据点
		对每个质心
			计算质心与数据点间的距离
		将数据点分配到距离其最近的簇
	对每个簇，计算簇中所有点的均值向量，并将值作为质心

使用Python建立k-means过程：

from numpy import *

def loadDataSet(fileName):      #导入tab分隔文件
    dataMat = []                #assume last column is target value
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float,curLine)) #此处map前加一个list才保证不出错
        dataMat.append(fltLine)
    return dataMat

def distEclud(vecA, vecB):       #计算点之间的欧式距离
    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)

def randCent(dataSet, k):        #随机选取质心
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))#create centroid mat
    for j in range(n):#create random cluster centers, within bounds of each dimension
        minJ = min(dataSet[:,j]) 
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
    return centroids

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):#kmeans建立，输入数据集、簇个数
    m = shape(dataSet)[0]#样本个数
    clusterAssment = mat(zeros((m,2)))#存放聚类的类别和距离值
    centroids = createCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:#当质心有所改变时持续循环
        clusterChanged = False
        for i in range(m):#对于每个数据点分配最近的质心
            minDist = inf; minIndex = -1
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2
        print (centroids)
        for cent in range(k):#更新质心
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster
            centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean 
    return centroids, clusterAssment

2.2 优缺点及适用性分析

优点：便于实现

缺点：可能收敛到局部最小值，在大规模数据上收敛较慢

3. 二分K-均值算法(bisecting K-means)

由于传统的KMeans算法的聚类结果易受到初始聚类中心点选择的影响，因此在传统的KMeans算法的基础上进行算法改进，对初始中心点选取比较严格，各中心点的距离较远，这就避免了初始聚类中心会选到一个类上，一定程度上克服了算法陷入局部最优状态。 二分KMeans(Bisecting KMeans)算法的主要思想是：首先将所有点作为一个簇，然后将该簇一分为二。之后选择能最大限度降低聚类代价函数（也就是误差平方和SSE）的簇划分为两个簇。以此进行下去，直到簇的数目等于用户给定的数目k为止。以上隐含的一个原则就是：因为聚类的误差平方和能够衡量聚类性能，该值越小表示数据点越接近于他们的质心，聚类效果就越好。所以我们就需要对误差平方和最大的簇进行再一次划分，因为误差平方和越大，表示该簇聚类效果越不好，越有可能是多个簇被当成了一个簇，所以我们首先需要对这个簇进行划分。

def biKmeans(dataSet, k, distMeas=distEclud):
    m = np.shape(dataSet)[0]
    clusterAssment = np.mat(np.zeros((m,2)))
    centroid0 = np.mean(dataSet, axis=0).tolist()[0]
    centList =[centroid0] #create a list with one centroid
    for j in range(m):#calc initial Error
        clusterAssment[j,1] = distMeas(np.mat(centroid0), dataSet[j,:])**2
    while (len(centList) < k):
        lowestSSE = np.inf
        for i in range(len(centList)):
            ptsInCurrCluster = dataSet[np.nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
            sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum
            sseNotSplit = sum(clusterAssment[np.nonzero(clusterAssment[:,0].A!=i)[0],1])
            print ("sseSplit, and notSplit: ",sseSplit,sseNotSplit)
            if (sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[np.nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
        bestClustAss[np.nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        print ('the bestCentToSplit is: ',bestCentToSplit)
        print ('the len of bestClustAss is: ', len(bestClustAss))
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids 
        centList.append(bestNewCents[1,:].tolist()[0])
        clusterAssment[np.nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE
    return np.mat(centList), clusterAssment

4.K-均值算法实战：对地图上的点进行聚类

这次没有选择《机器学习实战》课本上的案例，而是选取了2016.12.22周四00:00-00:30之间上海市出租车订单数据中所有正常数据的订单起始点进行聚类（总共137个数据点，数据来源是上学期交通地理信息系统课程）。此外还使用了上海市的路网shp文件，借助geopandas、numpy、matplotlib、pandas等模块，完成这些起始点的聚类，通过此过程我们可以看到热点地区的分布情况。

通过调用clusterOrders(numClust)即可进行进行以上聚类过程，此部分源代码如下，此外还需导入randCent()，kMeans()，biKmeans()函数。

def distSLC(vecA, vecB):#由经纬度转化为距离
    a = np.sin(vecA[0,1]*np.pi/180) * np.sin(vecB[0,1]*np.pi/180)
    b = np.cos(vecA[0,1]*np.pi/180) * np.cos(vecB[0,1]*np.pi/180) * \
                      np.cos(np.pi * (vecB[0,0]-vecA[0,0]) /180)
    return np.arccos(a + b)*6371.0 
import matplotlib
import pandas as pd
import matplotlib.pyplot as plt
import geopandas as gpd
route=gpd.read_file('SHMAP_Main.shp')#导入路网shp文件

def clusterOrders(numClust=5):      ##对订单进行聚类
    datList = []
    data = pd.read_csv('Thursdaymidnight.csv')  ##导入订单数据
    location = data[['s_long','s_la']] #使用订单的起点经纬度数据
    inner=[]
    for i in range(location.shape[0]):
        for j in [0,1]:
            a=location.iloc[i][j]
            inner.append(a)
        datList.append(inner)
        inner=[]
    datMat = np.mat(datList)    
    myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSLC) #调用二分K-均值算法进行聚类
    fig = plt.figure(figsize=(9,15))
    rect=[0.1,0.1,0.8,0.8]
    scatterMarkers=['s', 'o', '^', '8', 'p', \
                    'd', 'v', 'h', '>', '<']
    axprops = dict(xticks=[], yticks=[])
    ax0=fig.add_axes(rect, label='ax0', **axprops)
    route.plot(ax=ax0,color='darkgrey',alpha=0.2)  #绘制路网
    for i in range(numClust):
        ptsInCurrCluster = datMat[np.nonzero(clustAssing[:,0].A==i)[0],:]
        markerStyle = scatterMarkers[i % len(scatterMarkers)]
        ax0.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=60) #绘制订单数据点
    ax0.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300,color='k') #绘制质心
    plt.show()

尝试簇的数目由2至9，得到的聚类结果如下图所示：

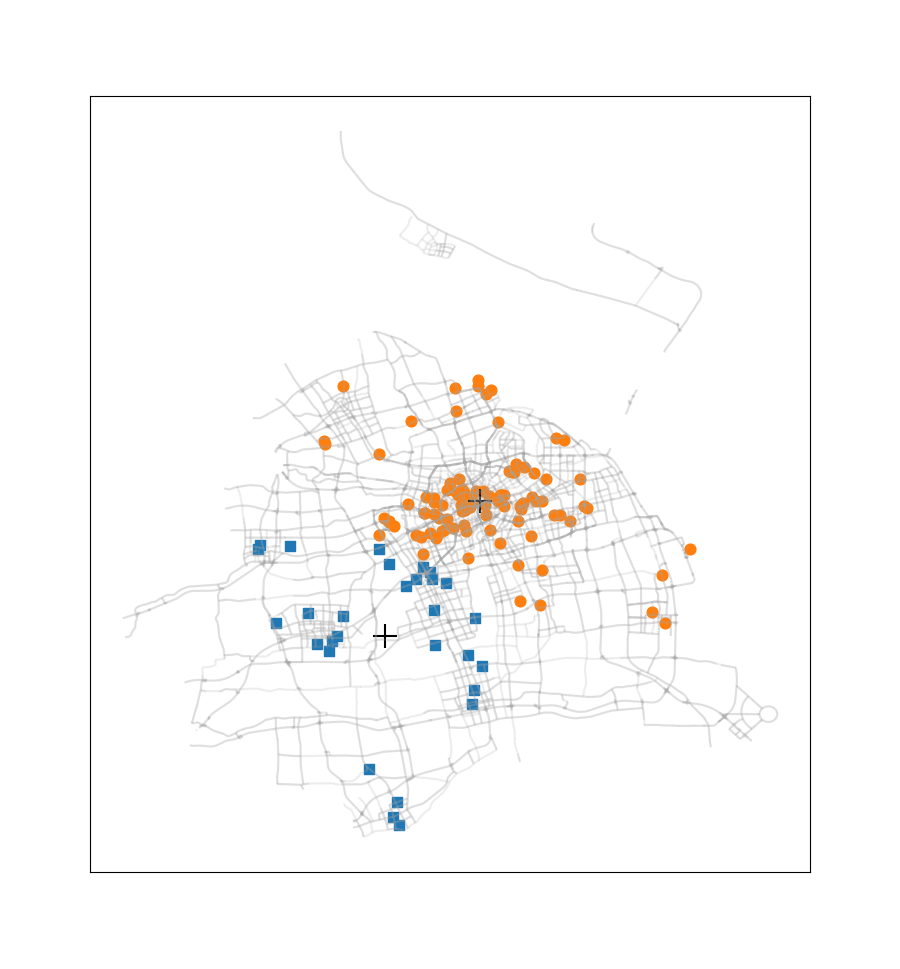
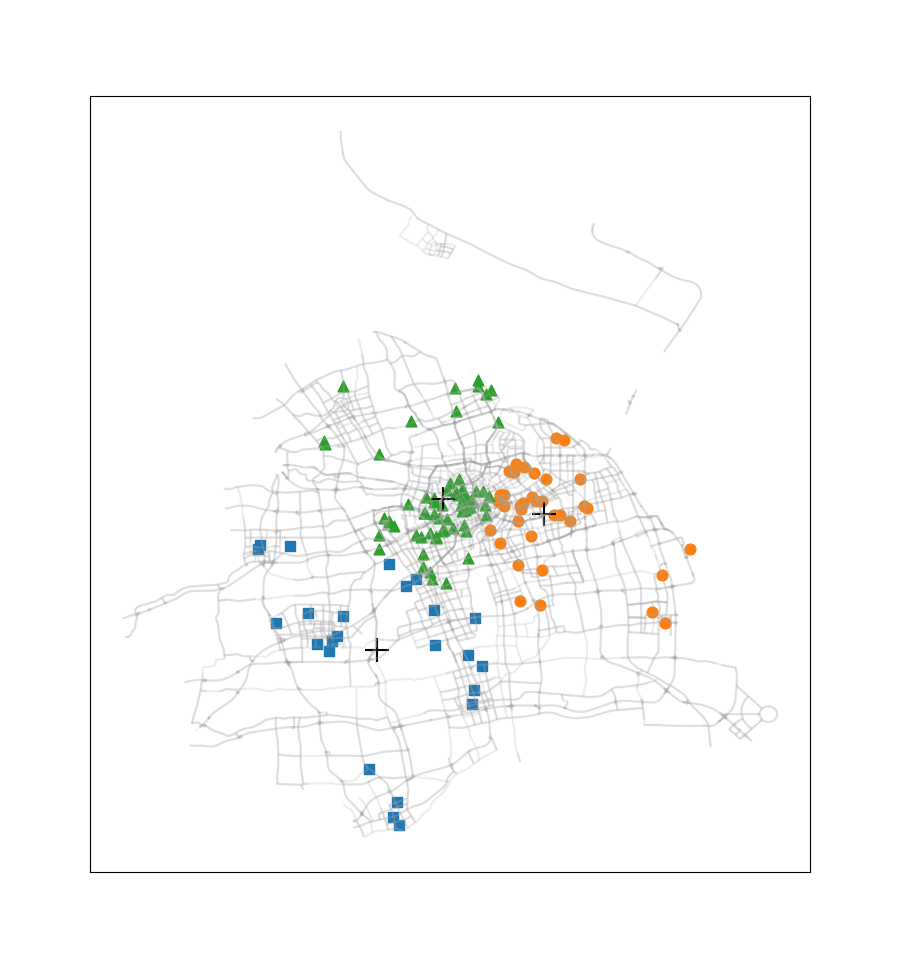
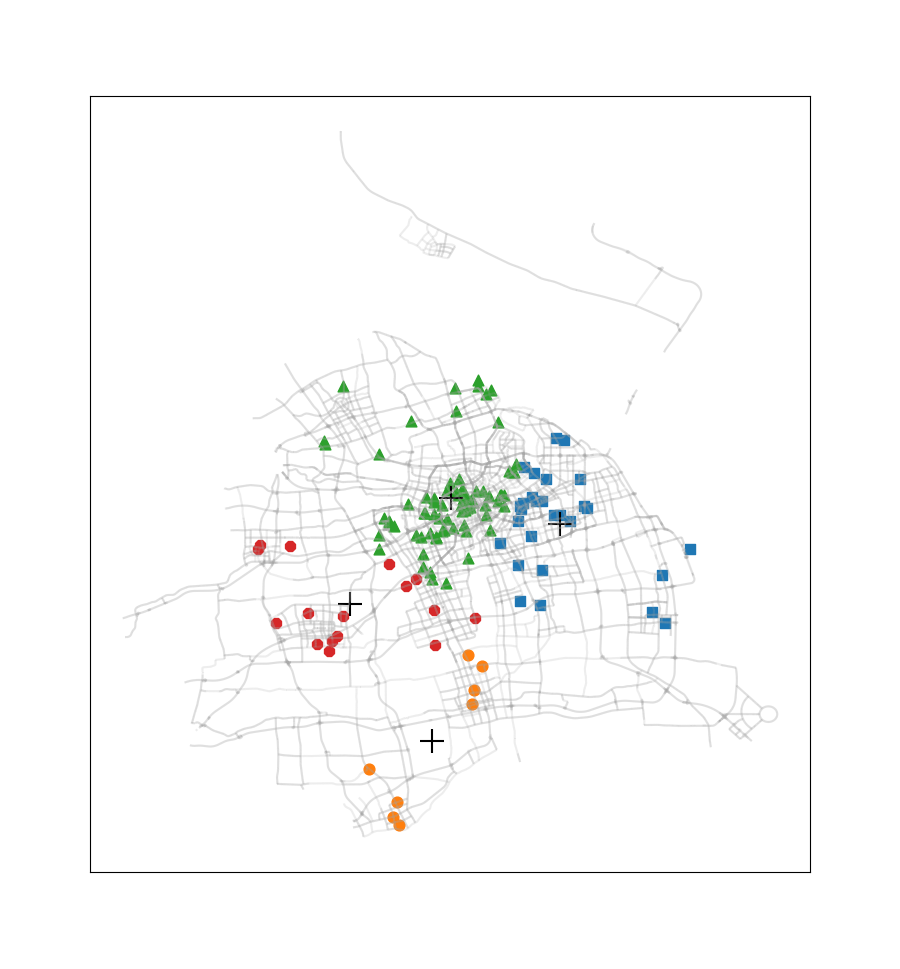
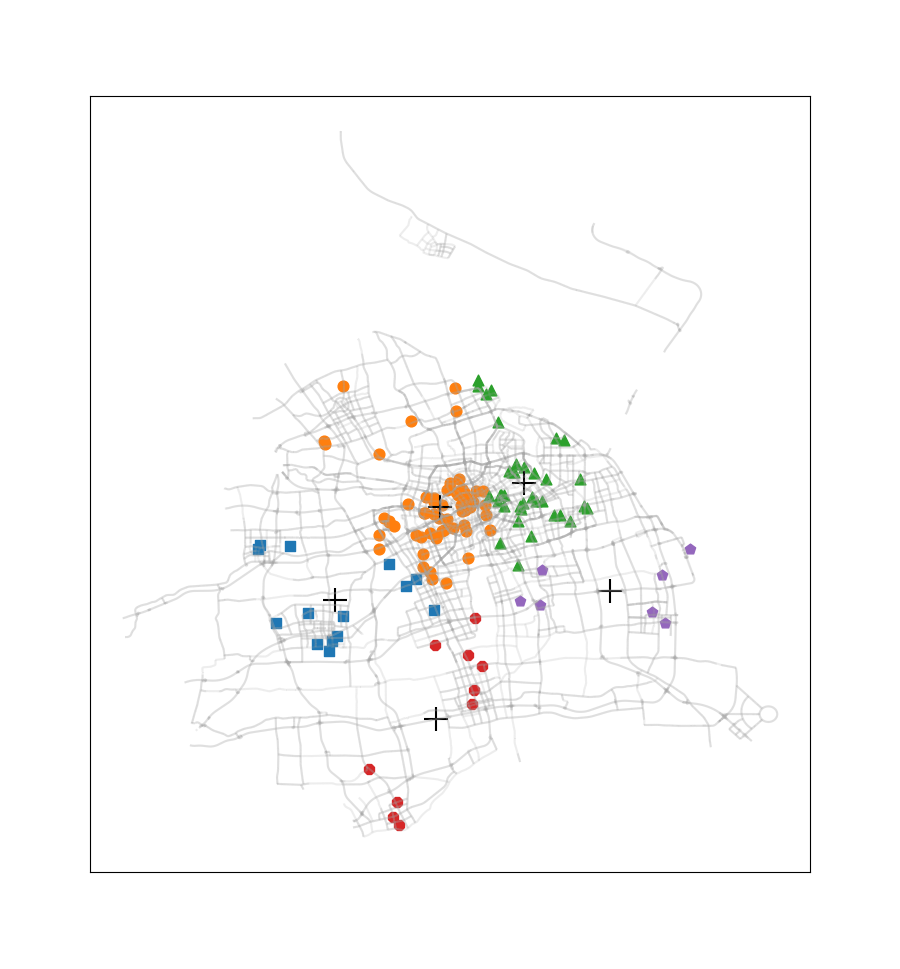
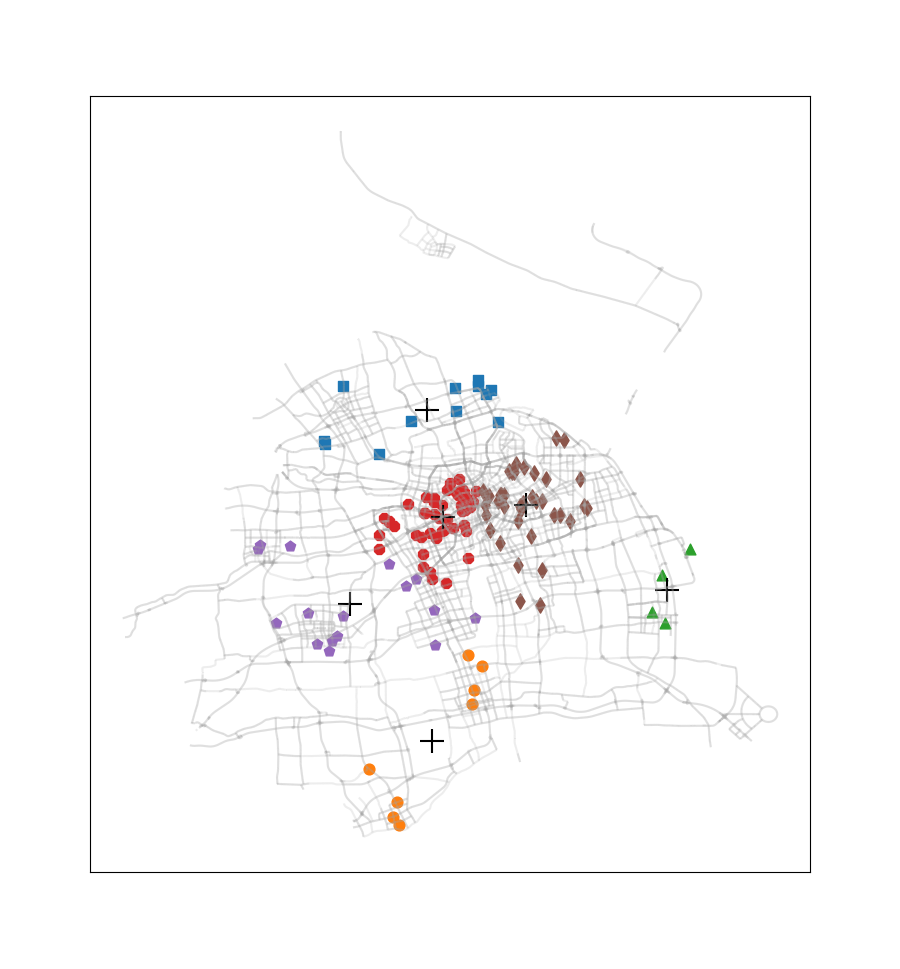
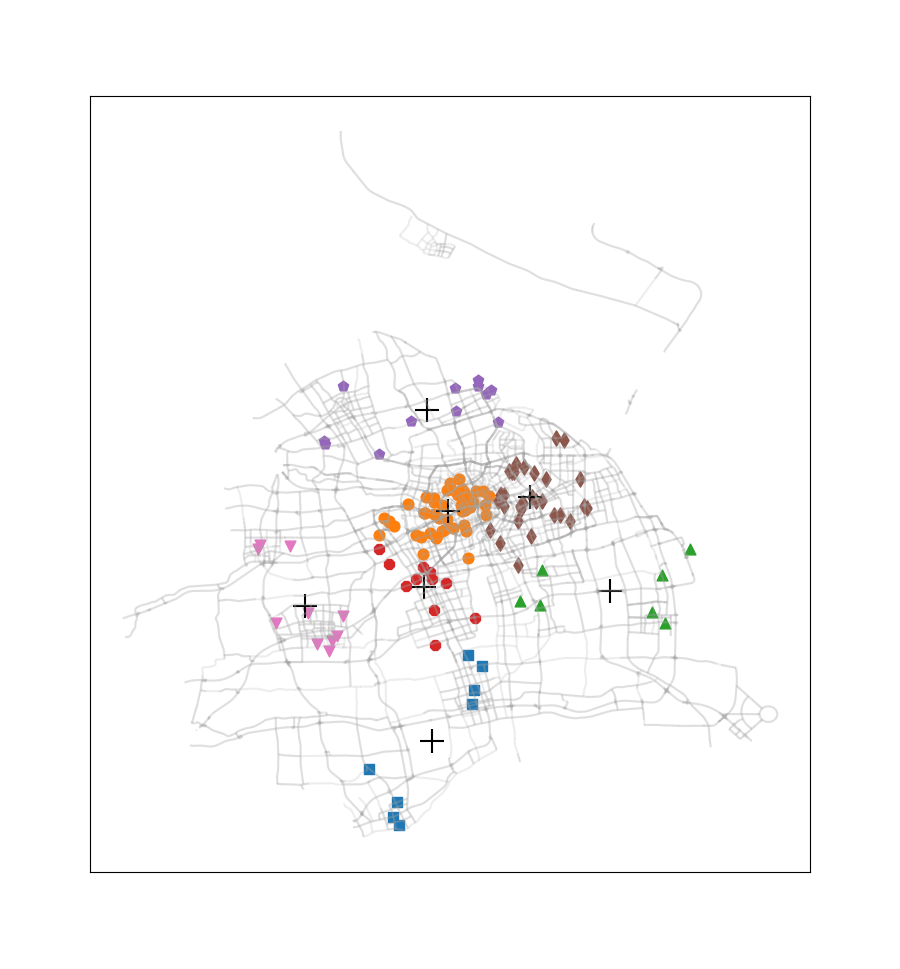
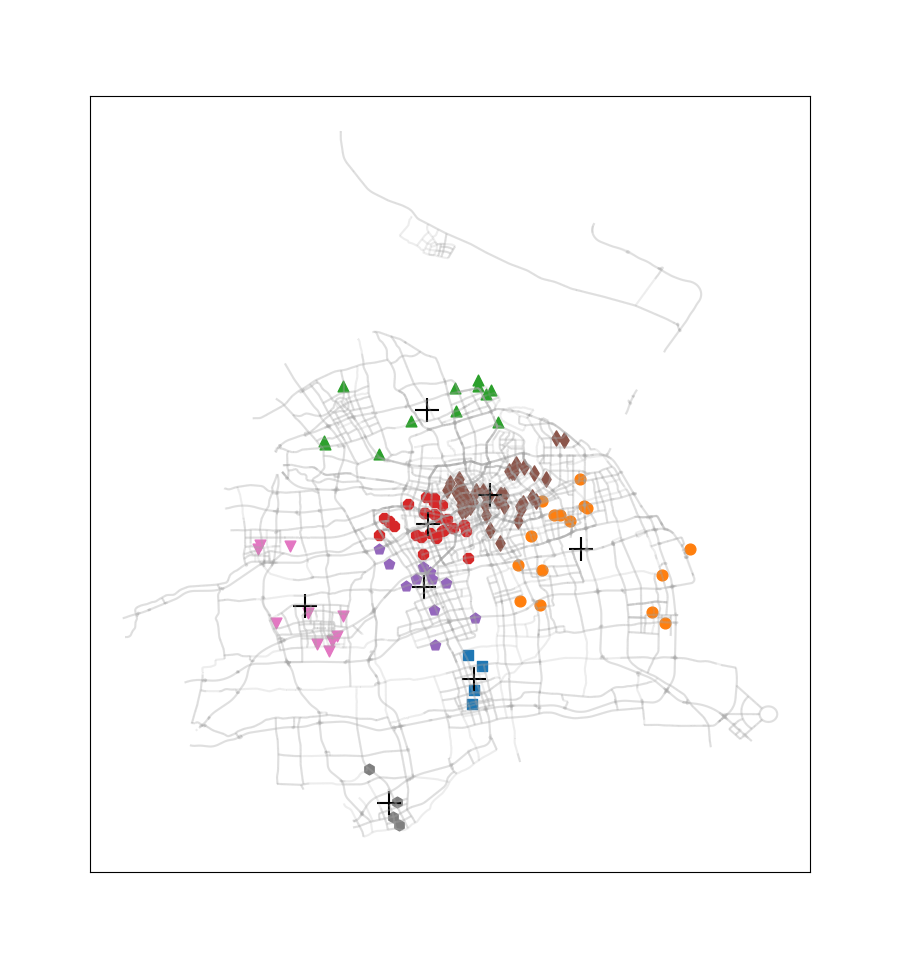
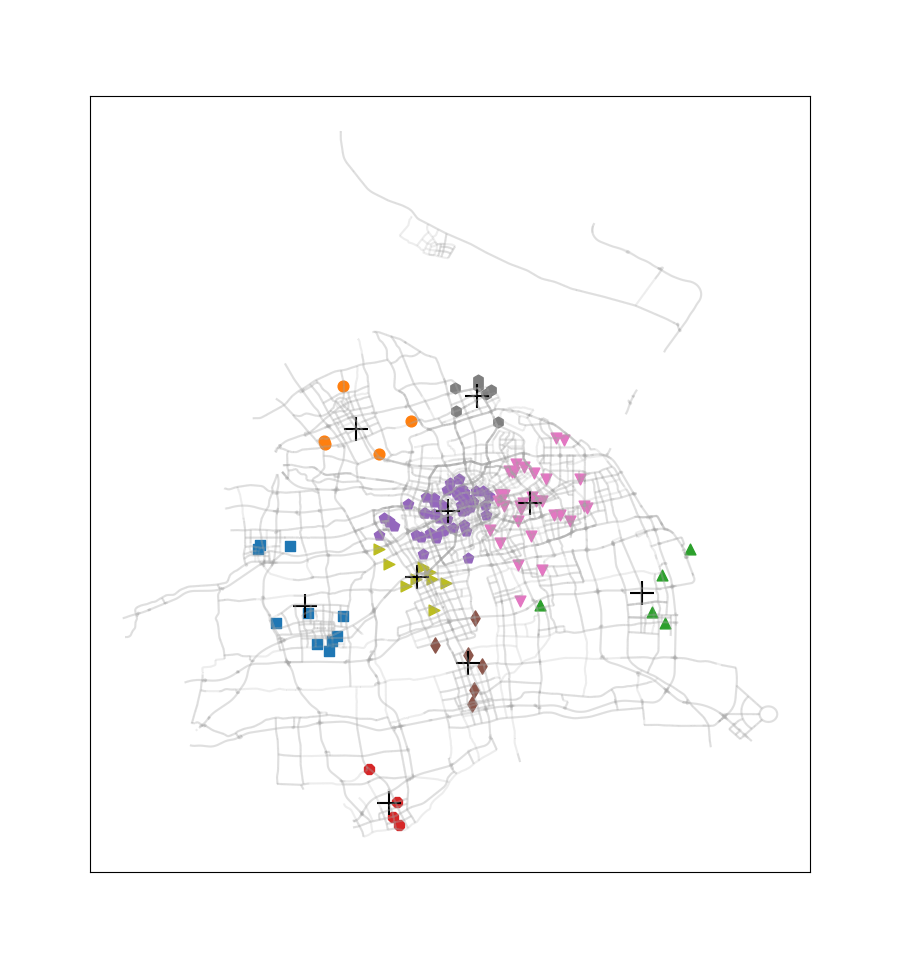
此案例只应用了非常少量的一部分订单数据，在应用于量较大的订单数据时，我们可以不绘制各个订单起始点，而是将每一簇的数目与簇质心‘+’符号的尺寸产生关联，使热点区域的显示更为直观。

关于原型聚类中的GMM高斯混合模型聚类、密度聚类与层次聚类由于内容较多，推导较为复杂，本篇内就不再详细叙述，GMM大概会与EM算法一起写一篇吧！

参考资料

周志华《机器学习》第9章
《机器学习实战》第10章
很多很多没有记录下来的博客