使用机器学习分析出租车订单数据

内容提要：

出租车轨迹、订单数据特点
使用回归方法补全缺失量较大的数据
利用DBSCAN方法对出租车订单数据进行聚类
使用Python进行地理信息分析与可视化
小记geopandas、osmnx、networkx、folium等gis模块问题描述

1. 问题背景

交通研究中，基础数据的获取尤为重要。数据获取方式近年来也有着天翻地覆的变化。

以获取出行者OD(origin, destination)的OD调查为例，获取OD能够定位城市各区域的交通发生与吸引情况，从而进行交通规划、城市管理等工作。传统OD获取方法如问卷调查法面向范围小、耗费人力物力、结果准确性差。随着含有GPS等传感器的智能手机的不断普及，与互联网经济的快速发展，滴滴、摩拜、高德等企业在运营中获取到了大量数据，这些数据获取难度小，覆盖范围广，采用“众包”的思路即获取到大量可以用于交通研究并指导实践，从而达到缓解城市交通拥堵的目的。

本次，我将利用订单数据(反映OD)进行空间聚类，从而利用出租车上下车点的数量、密度，识别城市的热点地区，进行交通生成的时空分析。

2. 出租车轨迹与订单数据

目前部分公司通过申请途径开放的数据主要有轨迹数据与订单数据两类。轨迹数据每隔一定的时间(约6-10s)记录一次，订单数据则每完成一个订单为一条记录。

本次选用2016.12.22周四上海市一天的订单数据进行分析，由于未能获取到能多数据，本案例旨在抛砖引玉，并记录与地理信息相关数据的处理方法。

2.1 订单数据

以下是本次使用的订单数据的字段：

字段描述	字段名称	说明
订单ID	order_id	随机生成，已加密
司机ID	driver_id	随机生成，已加密
车辆ID	car_id	已加密
城市名称	Shanghai
订单起点经度	s_long	保留5-6位小数
订单起点纬度	s_la	保留5-6位小数
订单终点经度	e_long	保留5-6位小数
订单终点纬度	e_la	保留5-6位小数
开始计费时间	s_time	%m%d%Y %H%M
订单完成时间	e_time	%m%d%Y %H%M
产品线	product	taxi
行程ID	route	taxi此字段默认0

订单数据可以用于分析但不限于：

订单时空数据分析（分不同的时段、区域，分析OD数据特征）但由于订单数据可能会被手动提前停止，因此并非全完准确。
车辆运营状况分析（追踪加密后的车辆id）
结合其他信息进行分析……

2.2 轨迹数据

轨迹数据相比订单数据，数据量大，包含更多有价值信息，可以进行更多的分析。

以下是轨迹数据通常提供的数据字段，也可能采集如加速度、陀螺仪角度等其他数据：

字段描述	说明
订单id	已加密
轨迹点对应的时间戳
相应坐标经度
相应坐标纬度
相应瞬时速度
乘客状态	1/0

轨迹数据可以用于分析但不限于：

通过抽取起终点，能够分析订单数据所得到的信息
分析不同类型车辆（出租车、快车）的行驶特点
分析不同行驶状态（空驶、载人）时的行驶特点
估计道路交通状况
3. 数据预处理

针对原始数据，首先需要进行数据预处理工作：

可以使用绘图、统计量分析、相关性分析等的手段，其中绘图可以借助Python的matplotlib库，统计量分析可以使用pandas自带的分析功能，相关性分析可以借助scikit-learn库的相关功能。

使用sklearn进行特征工程
Pandas统计分析
Matplotlib tutorial
3.1 导入模块、数据、查看异常数据

#导入所需要的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import geopandas as gpd
import osmnx as ox
import time
from geopandas.tools import sjoin
import datetime
from math import radians, cos, sin, asin, sqrt
plt.style.use('ggplot')

由于数据不存在缺失（空缺），未记录的“订单结束时间e_time”被记录为’0000-00-00 00:00:00’，因此在此查看未正确记录的数据量。以下结果表明，问题数据量达近30%，需采用一定手段进行处理。

Thurdata=pd.read_csv('THURSDAY.csv')
#判断是否是问题数据，并添加属性列
Thurdata['judge'] = Thurdata.e_time.apply(lambda x: 1 if x=='0000-00-00 00:00:00' else 0) 
#查看问题数据量
Thurdata['judge'].value_counts()

0    18568
1     7072
Name: judge, dtype: int64

目前缺失值、异常值的主要处理手段有：

删除异常值——此处由于异常值量较多，直接删除会造成结果偏差
采用前、后值填补——由于订单数据间不存在关联性，此方法不合适
采用均值填充——可以采用‘开始时间+平均时间间隔’的方式来填充
采用其他关系填充

3.2 异常数据的筛选与结束时间的回归补全

在本步骤中：

Step1：对于结束时间e_time正常的数据，计算通行时间 $time_interval=e_time-s_time$；结束时间e_time异常的数据，采用np.nan填充

Step2：查看通行时间数据特点，删除通行时间异常的数据（time_intervel<180s或time_interval>14400s）

Step3：计算起终点间直线距离（经纬度距离计算公式）

Step4：查看起终点间直线距离的特点，删除直线距离异常的数据（LineDistance<10m或linedistance>100km）

Step5：回归分析直线距离与通行时间的关系，并利用回归公式填充结束时间e_time异常的数据

Step6：借助地理信息计算路网中起终点间的最短路，并记录。

Step7：回归分析路网最短距离与通行时间的关系，并利用回归公式重新填充结束时间e_time异常的数据，整合正常数据与填充异常结束时间值的数据

Step1 计算通行时间

def dataInterval(data1,data2):
    d1 = datetime.datetime.strptime(data1,'%m/%d/%Y %H:%M')#字符串形式转化为DateTime形式
    d2 = datetime.datetime.strptime(data2,'%m/%d/%Y %H:%M')
    delta = d2 - d1
    return delta.seconds#将timedelta转化为秒计数

def getInterval(arrLike):  #用来计算通行时间调用的函数
    s_time = arrLike['s_time']
    e_time = arrLike['e_time']
    error = arrLike['judge']
    if error==0:#正常数据
        interval = dataInterval(s_time.strip(),e_time.strip())  #去掉两端空白
    else:#问题数据
        interval = np.nan
    return interval
Thurdata['TimeInterval'] = Thurdata.apply(getInterval,axis=1)#时间差计算

Step2 查看通行时间特点，删除异常数据

1 2	timeinterval=np.array(Thurdata['TimeInterval']) timeinterval = np.sort(timeinterval[~np.isnan(timeinterval)])#将非空数据找出并进行排序

plt.plot(timeinterval,'.')
plt.ylabel('timeinterval(s)')
plt.xlabel('sample')
plt.title('Timeinterval of all the samples');#时间间隔

png

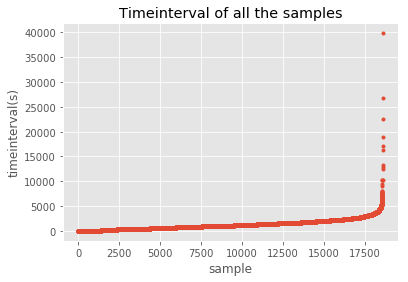
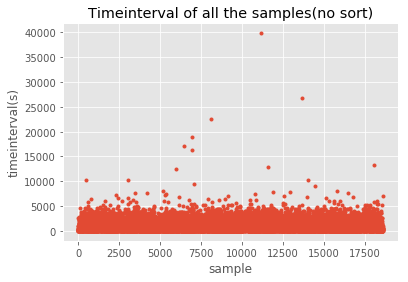
将通行时间排序后绘图，不难发现随着样本数量的变化，时间间隔增加先处于平稳状态而后激增。绘制未排序的时间间隔散点图也可以发现，大部分记录通行时间均在8000s以内，考虑上海市地理状况与采取出租出行的实际状况，同时考虑样本数量，我们去除[0,180s]与14400s及以上的数据。

项目	通行时间t<180或t>14400s	通行时间180≤t≤14400s
样本数	1610	16958
占比	8.67%	91.33%

timeinterval=np.array(Thurdata['TimeInterval'])
timeinterval = timeinterval[~np.isnan(timeinterval)]
plt.plot(timeinterval,'.')
plt.ylabel('timeinterval(s)')
plt.xlabel('sample')
plt.title('Timeinterval of all the samples(no sort)');

png

timeinterval=np.array(Thurdata['TimeInterval'])
timeinterval = timeinterval[~np.isnan(timeinterval)]
c_ti=timeinterval[(timeinterval>180)&(timeinterval<14400)]#考虑可能的乘车时间（大于3min小于4小时）
plt.hist(c_ti,bins=50,edgecolor='black')#滤除时间间隔
plt.xlabel('timeinterval')
plt.ylabel('numberofsample(s)')
plt.title('The histogram of the normal Timeinterval(180s,14400s)');

png

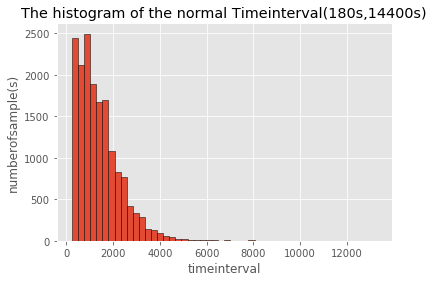
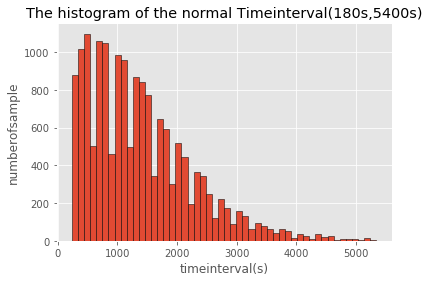
分别绘制通行时间在(180s,14400s)与(180s,5400s)区间范围内的分布直方图，从图中我们可以进一步看到，通行[500s,900s]区间内的样本数较多，随着通行时间的增加，总体样本数呈现由较高水平先增加后减小的趋势。(bins=100效果更明显)

timeinterval=np.array(Thurdata['TimeInterval'])
timeinterval = timeinterval[~np.isnan(timeinterval)]
c_ti=timeinterval[(timeinterval>180)&(timeinterval<5400)]#考虑可能的乘车时间（大于3min小于4小时）
plt.hist(c_ti,bins=50,edgecolor='black')#滤除时间间隔
plt.xlabel('timeinterval(s)')
plt.ylabel('numberofsample')
plt.title('The histogram of the normal Timeinterval(180s,5400s)');

png

Step3 直线距离计算

采用Haversine formula公式，利用两点经纬度坐标，计算距离。并将直线距离写入数据表的‘LD’列。

def countdistance(long1,la1,long2,la2):#地球上直线距离的计算
    #deltasigma=np.arctan(np.sqrt((np.cos(la2)*np.sin(long2-long1))**2+(np.cos(la1)*np.sin(la2)-np.sin(la1)*np.cos(la2)*np.cos(long2-long1))**2)/(np.sin(la1)*np.sin(la2)+np.cos(la1)*np.cos(la2)*np.cos(long2-long1)))
    #lineardistance=6372.795*deltasigma 
    long1, la1, long2, la2 = map(radians, [long1, la1, long2, la2])  
    dlong = long2 - long1   
    dla = la2 - la1   
    a = sin(dla/2)**2 + cos(la1) * cos(la2) * sin(dlong/2)**2  
    c = 2 * asin(sqrt(a))   
    r = 6371.0088 # 地球平均半径，单位为公里 
    lineardistance=c * r * 1000 #精度为m
    return lineardistance
def getLD(arrLike):  #指定df调用距离计算函数
    long1 = arrLike['s_long']
    la1 = arrLike['s_la']
    long2 = arrLike['e_long']
    la2 = arrLike['e_la']
    LD = countdistance(long1,la1,long2,la2)  
    return LD
Thurdata['LD'] = Thurdata.apply(getLD,axis=1)

Step4 查看直线距离特点，删除异常数据

采用与通行时间相同的分析方式，对于订单数据每条的起终点间距离进行分析，数据变化趋势与通行时间大致相同。指定直线距离(10m,100km)范围内的为正常数据。

项目	直线距离l<10m或l>100km	直线距离10m≤l≤100km
样本数	5	25635
占比	0.02%	99.98%

plt.plot(Thurdata['LD'],'.',c='royalblue',alpha=0.6)
plt.ylim(10,100000)
plt.xlabel('sample')
plt.ylabel('LineDistance(m)')
plt.title('LineDistance of all normal(10m,100km) samples(no sort)');

png

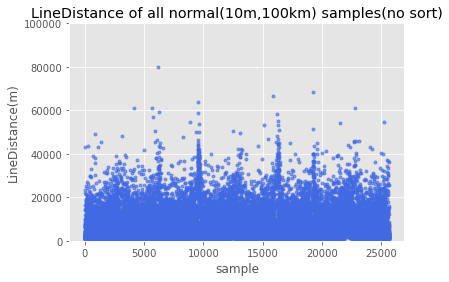
LineDistance=np.array(Thurdata.LD)
distance =np.sort(LineDistance[(LineDistance<100000)&(LineDistance>10)])
plt.plot(distance,'.',c='royalblue')
plt.xlabel('sample')
plt.ylabel('LineDistance(m)')
plt.title('LineDistance of all normal(10m,100km) samples');

png

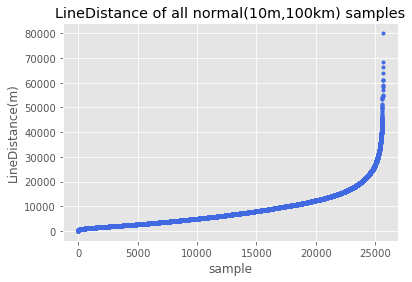
plt.hist(distance,bins=50,facecolor='royalblue',edgecolor='k')#滤除时间间隔
plt.ylabel('numberofsample')
plt.xlabel('LineDistance(m)')
plt.title('The histogram of the normal LineDistance(10m,100km)');

png

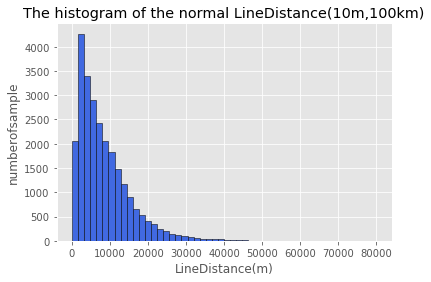
Step5 回归分析直线距离与通行时间之间的关系

在以上分析中，我们不难推测距离与通行时间可能存在一定线性关系。这一推测在实际运用中不难解释，在不考虑拥堵等外部因素影响及圈运行的情况下，距离约远，通行时间越长。

筛选正常数据用于回归(正常的含义：timeinterval、LineDistance、endtime正常)

1	Regdata=Thurdata.loc[(Thurdata.LD<100000)&(Thurdata.LD>10)&(Thurdata.TimeInterval<14400)&(Thurdata.TimeInterval>180)]

计算各个变量间的相关系数，通行时间与直线距离间的相关系数达0.708670，可见二者相关性强。因此，选取直线距离与通行时间进行线性回归，并通过此线性回归关系填补异常的结束时间数据。

#正常数据的直线距离与通行时间散点分布图
plt.plot(Regdata.LD,Regdata.TimeInterval,'.',c='k',alpha=0.6)
plt.xlabel('LineDistance')
plt.ylabel('timeinterval')
plt.title('The relationship between LineDistance and Timeinterval');

png

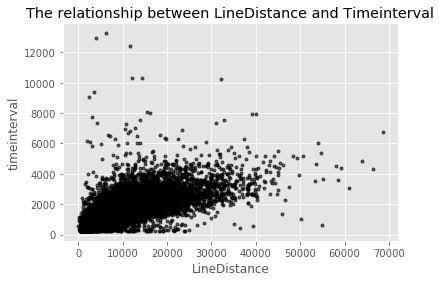
可以使用sklearn的回归函数功能进行回归分析，此时R方约为0.5，回归效果如下图所示：

from sklearn.linear_model import LinearRegression
#regr为回归过程，fit(x,y)进行回归  
x=np.array(Regdata.LD).reshape(-1, 1)
y=np.array(Regdata.TimeInterval).reshape(-1, 1)
regr = LinearRegression().fit(x,y)   
plt.plot(x,y,'.',color='black',alpha=0.6)  
#用predic预测，这里预测输入x对应的值，进行画线  
plt.plot(x, regr.predict(x), color='red', linewidth=1);

png

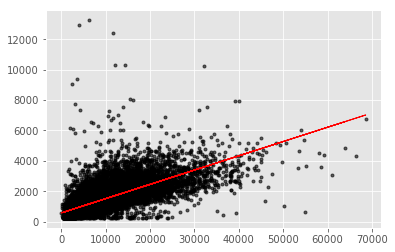
此时我们可以，利用以上线性回归关系，预测出行时间，与starttime求和得到endtime，将缺失endtime的问题数据补全。之后将原本的正常数据（范围正常、无缺失）与补全后的问题数据合并得到新数据。

1
2
3

errordata=Thurdata.loc[(Thurdata.judge==1)&(Thurdata.LD<100000)&(Thurdata.LD>10)]
errordata.loc[:,'TimeInterval']=regr.predict(np.array(errordata.LD).reshape(-1, 1))#注意使用sklearn需要reshape
errordata.TimeInterval= errordata.TimeInterval.apply(np.round)

def fillendtime(data1,interval):
    d1 = datetime.datetime.strptime(data1,'%m/%d/%Y %H:%M')
    delta = datetime.timedelta(seconds=interval)
    d2 = d1 + delta
    d2 = d2.strftime('%m/%d/%Y %H:%M')
    return d2

def getendtime(arrLike):  #用来计算日期间隔天数的调用的函数
    s_time = arrLike['s_time']
    interval = arrLike['TimeInterval']
    e_time = fillendtime(s_time.strip(),interval)  #注意去掉两端空白
    return e_time
errordata['e_time'] =errordata.apply(getendtime,axis=1)#结束时间
Thursnewdata = pd.concat([Regdata,errordata])
# Thursnewdata.to_csv('ThursuseLD.csv')   #保存现状csv文件

（PS：由于路网规模较大，以下求算最短路过程大约需要4-5小时,因此可直接跳过以下回归步骤进入聚类部分)

Step6 结合地理信息(路网)求算两点间的最短路网距离

由于两点间的直线距离与两点间通过路网连通的实际距离存在差异，因此考虑结合实际的GIS信息数据，寻找起终点间的最短路网距离。并试图建立路网最短距离与通行时间之间的关系，从而填补异常数据。

使用第三方模块osmnx可以帮助我们在线获取某一区域的底图。获取上海市路网，此过程大约用时20min，时间与路网规模有关。获取所得的网络如下图所示。可以保存为shp或SVG等格式的文件以便下次使用。

1
2
3

place = 'Shanghai,China'
Shanghai = ox.graph_from_place(place,which_result=2)
ox.plot_graph(Shanghai)

png

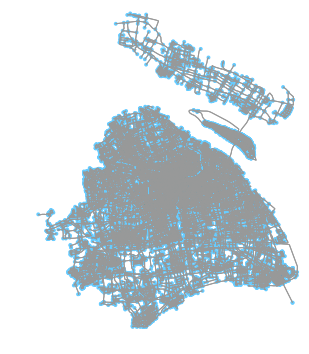
networkx第三方模块给了我们求算路网间两点最短路的工具，因此我们需要进行：

Step1：地图匹配：找到位于路网上的与起终点距离最近的点

Step2：计算最短距离：计算Step1中路网上两点间的距离

start_long = np.array(Thursnewdata.s_long).reshape(-1,1)
start_la = np.array(Thursnewdata.s_la).reshape(-1,1)
end_long = np.array(Thursnewdata.e_long).reshape(-1,1)
end_la = np.array(Thursnewdata.e_la).reshape(-1,1)

import networkx as nx
shortestroutelength=[]
for i in range(start_long.shape[0]):
    origin_point = (start_la[i][0], start_long[i][0])
    destination_point = (end_la[i][0], end_long[i][0])
    origin_node = ox.get_nearest_node(Shanghai, origin_point)
    destination_node = ox.get_nearest_node(Shanghai, destination_point)
    try:
        length = nx.shortest_path_length(Shanghai, origin_node, destination_node, weight='length')
    except Exception as e:
        shortestroutelength.append(-1)
    else:
        shortestroutelength.append(length)

1 2	Thursnewdata.SD = shortestroutelength #Thursnewdata.to_csv('ThursSD.csv') #保存最短路计算结果文件

Step7 回归分析路网最短距离与通行时间的关系并填充异常数据

以下回归过程与Step5同理。

Regdata2=Thursnewdata.loc[Thursnewdata.judge==0]#挑选正常数据用于回归
x2=np.array(Regdata2.SD).reshape(-1, 1)
y2=np.array(Regdata2.TimeInterval).reshape(-1, 1)
regr2 = LinearRegression().fit(x2,y2)    
plt.plot(x2,y2,'.',color='black',alpha=0.6)  
#用predic预测，这里预测输入x对应的值，进行画线  
plt.plot(x2, regr2.predict(x2), color='g', linewidth=1);

png

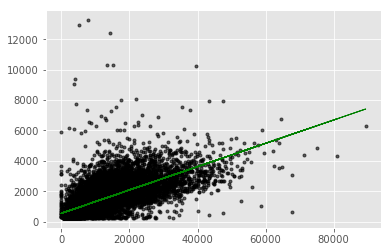
errordata2=Thursnewdata.loc[Thursnewdata.judge==1]
errordata2.loc[:,'TimeInterval']=regr2.predict(np.array(errordata2.SD).reshape(-1, 1))#注意使用sklearn需要reshape
errordata2.TimeInterval= errordata2.TimeInterval.apply(np.round)
errordata2['e_time'] =errordata2.apply(getendtime,axis=1)#结束时间
ThursnewdataSD = pd.concat([Regdata2,errordata2])
# ThursnewdataSD.to_csv('ThursuseSD.csv')

4. 聚类分析

4.1 聚类方法选取

划分方法（如K均值与K中心点算法）：每个对象至少属于一个簇，需提前指定划分簇的数量，簇数量少时，不能准确反映热点区域位置；簇数量多时，效果可观。但不太适用于数据量大的数据集。且噪声数据在一定程度上影响结果。
层次方法：需指定如簇间距或簇数量等终止条件。据《交通地理信息系统技术与前沿发展》一书中所写道：

分析出租车轨迹数据具有一定探索性，因此选用层次聚类分析方法比较合适，相似性度量方法有单连接方法、完全连接方法、平均连通方法、中心点连通方法等，单连接算法有“链条现象”的缺陷。但是对于分布在路网上的车辆而言，行驶在同一路段上的车辆应该具有相同或相似的目的地……使用单连接的度量方法更佳。
基于密度的方法：基本思想：对于簇内的每个数据点，一定半径范围ep内必须包含一定数量的点的个数min_samples。如DBSCAN可以用于发现任意形状的簇，并过滤噪声点。并非每个对象都属于一个簇。
基于网格的方法：划分网格结构，聚类在网格结构上进行。优点为速度快。
基于模型的方法：基于模型的方法主要有基于统计的方法与基于神经网络的方法。

4.2 使用DBSCAN方法进行不同时段的OD点聚类

基于以上方法分析，本次聚类采用DBSCAN的基于密度的方法，该方法被认为较为适合地点数据的聚类。该算法过程如下图所示，来源周志华《机器学习》。该过程可自行编程实现，也可以借助scikit-learn第三方库实现。

DBSCAN

导入数据，转换时间类型为DateTime

由于数据导入时，默认为字符串格式，无法进行时间的运算，因此需通过strp函数转化为DateTime时间戳格式。

#为了方便，以下开了一个新的notebook
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import geopandas as gpd
import osmnx as ox
import networkx as nx
import time
from geopandas.tools import sjoin
import datetime
plt.style.use('seaborn')
from sklearn.cluster import DBSCAN
from sklearn import metrics
import folium as f
from geopy.distance import great_circle
from shapely.geometry import MultiPoint

ThursnewdataSD=pd.read_csv('ThursuseSD.csv')
def changeDateTime(timestr):
    datetime1 = datetime.datetime.strptime(timestr,'%m/%d/%Y %H:%M')
    return datetime1
ThursnewdataSD['s_time'] = ThursnewdataSD.s_time.apply(changeDateTime)
ThursnewdataSD['e_time'] = ThursnewdataSD.e_time.apply(changeDateTime)

筛选出某一时段的数据

交通分析一般进行早高峰、晚高峰与平峰状态的分析，因此此处改动period参数即可改换随后的分析时段。

period = 'night'
def get_period_time(period):
    if period=='morning':
        period_of_time=['07:30','09:30']
    if period=='afternoon':
        period_of_time=['14:30','16:30']
    if period=='night':
        period_of_time=['15:30','19:30']
    return period_of_time

#判断某个时间段内的数据
TMO=ThursnewdataSD.loc[(ThursnewdataSD.s_time>(datetime.datetime.strptime('12/22/2016 %s'%(get_period_time(period)[0]),'%m/%d/%Y %H:%M')))&(ThursnewdataSD.s_time<(datetime.datetime.strptime('12/22/2016 %s'%(get_period_time(period)[1]),'%m/%d/%Y %H:%M')))]
TMD=ThursnewdataSD.loc[(ThursnewdataSD.e_time>datetime.datetime.strptime('12/22/2016 %s'%(get_period_time(period)[0]),'%m/%d/%Y %H:%M'))&(ThursnewdataSD.e_time<datetime.datetime.strptime('12/22/2016 %s'%(get_period_time(period)[1]),'%m/%d/%Y %H:%M'))]
coords1 = TMO.as_matrix(columns=['s_la', 's_long'])
coords2 = TMD.as_matrix(columns=['e_la', 'e_long'])
#合并为coords
coords=np.vstack((coords1,coords2))

使用DBSCAN聚类

DBSCAN算法主要涉及eps（半径）与min_samples（最少样本个数）两个参数，eps越小、min_samples越大，聚集的类的密度更高。

kms_per_radian = 6371.0088
epsilon = 1.5 / kms_per_radian
start_time = time.time()
db = DBSCAN(eps=epsilon, min_samples=30, algorithm='ball_tree', metric='haversine').fit(np.radians(coords))#epsilon与min_samples参数可调
#获取每个点的标签
cluster_labels = db.labels_
# 获取聚类簇的数目
n_clusters_ = len(set(cluster_labels)) - (1 if -1 in cluster_labels else 0)

# 聚类效果评价输出
message = 'Clustered {:,} points down to {:,} clusters, for {:.1f}% compression in {:,.2f} seconds'
print(message.format(coords.shape[0], n_clusters_, 100*(1 - float(n_clusters_) / coords.shape[0]), time.time()-start_time))
print('Silhouette coefficient: {:0.03f}'.format(metrics.silhouette_score(coords, cluster_labels)))

Clustered 9,504 points down to 19 clusters, for 99.8% compression in 1.04 seconds
Silhouette coefficient: -0.060

1	clusters = pd.Series([coords[cluster_labels==n] for n in range(n_clusters_)])#将聚类结果保存下来

确定聚类各个簇的中心

def get_centermost_point(cluster):
    centroid = (MultiPoint(cluster).centroid.x, MultiPoint(cluster).centroid.y)
    centermost_point = min(cluster, key=lambda point: great_circle(point, centroid).m)
    return tuple(centermost_point)
centermost_points = clusters.map(get_centermost_point)

绘制聚类结果

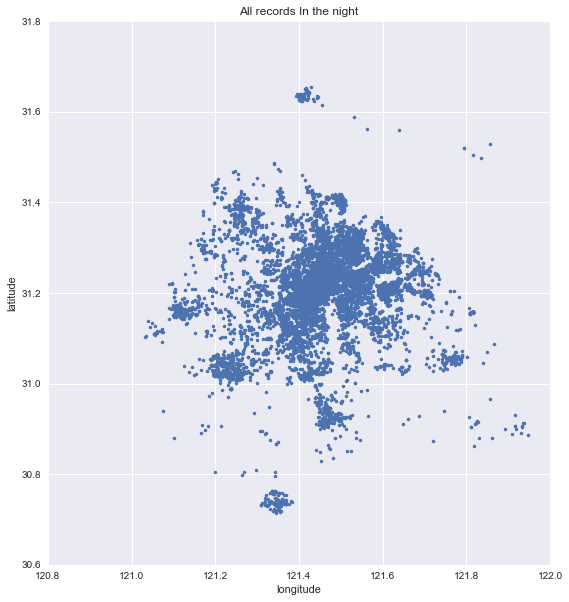
以下是采用eps = 1.5 / kms_per_radian；min_samples=30的条件下对当日晚高峰数据进行聚类得到的效果图。类中心标注了该类的样本个数。

colorbox=['lightblue','orange','red','blue','lawngreen','peru','gray','black','yellow','violet','purple','navy','gold','yellowgreen','cadetblue','midnightblue','hotpink','cyan','m','olive','green','grey','k']
plt.figure(figsize=(9,10))
for i in range(n_clusters_):
    X= coords
    one_cluster = X[cluster_labels == i]
    #print(one_cluster.shape[0])打印每个簇点的个数
    plt.text(centermost_points[i][1]-0.01,centermost_points[i][0]-0.01,'%s'%one_cluster.shape[0],fontdict={'size':10, 'color':'k'})
    plt.plot(one_cluster[:,1],one_cluster[:,0],'.',color='%s'%colorbox[i],label='Cluster:%s'%(i+1))
    plt.legend()
plt.xlim(120.8,122.0)
plt.ylim(30.6,31.8)
plt.title('Clusters In the %s'%period)
plt.xlabel('longitude')
plt.ylabel('latitude')
#plt.savefig('Clusters In the %s.jpg'%period);

png

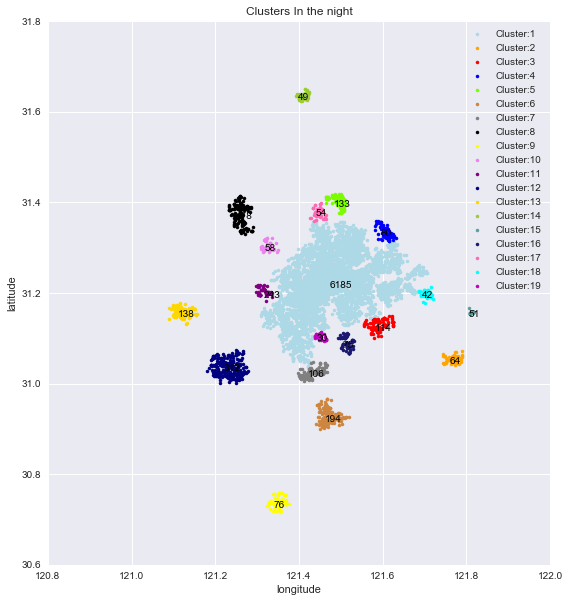
将如上图所示的聚类结果与聚类数据进行比对，可以对聚类的效果进行衡量。本次采用了“轮廓系数”这一参数进行衡量，它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。该系数1为最佳，-1为最差，但个人认为用于衡量本问题不太合适。

网络上有很多聚类的衡量方法，如有望继续讨论，可阅读scikit-learn的文档中有关聚类评价的内容。

plt.figure(figsize=(9,10))
plt.plot(coords[:,1],coords[:,0],'.')
plt.xlim(120.8,122.0)
plt.ylim(30.6,31.8)
plt.title('All records In the %s'%period)
plt.xlabel('longitude')
plt.ylabel('latitude')
#plt.savefig('All records In the %s.jpg'%period);

png

利用在线地图绘制聚类结果

仅用上述绘图方法不易与实际地理位置对应，因此采用folium库制作在线地图的方式显示结果。（但亲测数据量太大时会报错）

oneUserMap = f.Map(location=[30.917758, 121.806093])
for i in range(n_clusters_):
    X= coords
    one_cluster = X[cluster_labels == i]
    #print(one_cluster.shape[0])
    for j in range(one_cluster.shape[0]):
        color1=colorbox[i]
f.RegularPolygonMarker([one_cluster[j,0],one_cluster[j,1]],color='%s'%color1,fill_color='%s'%color1,radius=3,number_of_sides=8).add_to(oneUserMap)
oneUserMap

以下是除了除上海市城区无法绘制外其余的簇在早高峰时段的效果图。

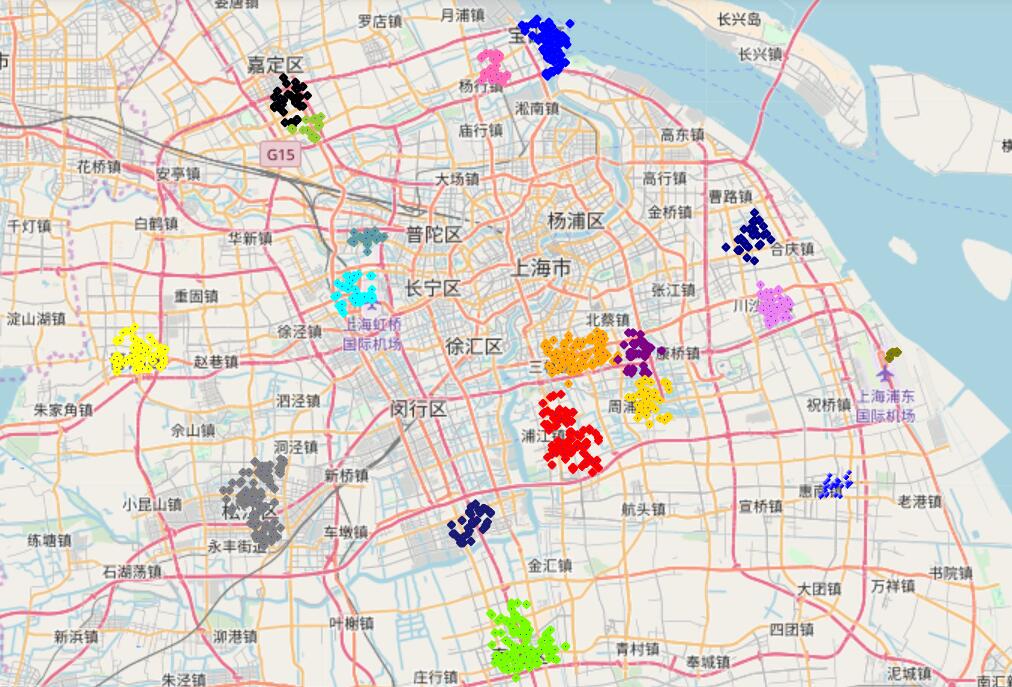
5. 利用MarkerCluster进行聚类与可视化

MarkerCluster是folium库下的插件之一，具有聚类与可视化的效果。其聚类与open street map在线地图结合，且随着地图尺度的变化可以动态显示聚类的效果与边界，同时对于大规模数据的运算速度较快，几乎没有卡顿现象（未查到准确、官方资料，猜测算法是利用基于网格的聚类方法完成）。且有众多可调节参数，可以依照需求进行调整。

1	from folium.plugins import MarkerCluster

location1=[]
location2=[]
for i in range(coords1.shape[0]):
    location1.append([float('%.6f'%(coords1[i,0])),float('%.6f'%(coords1[i,1]))])
for i in range(coords2.shape[0]):
    location2.append([float('%.6f'%(coords2[i,0])),float('%.6f'%(coords2[i,1]))])

m = f.Map(location=[30.917758, 121.806093])
marker_cluster = MarkerCluster(name='%s'%period)
for k in range(len(location1)):
    location = location1[k][0], location1[k][1]
    marker = f.Marker(location=location,icon=f.Icon(color='red'))
    popup = 'lon:{}<br>lat:{}'.format(location[1], location[0])
    f.Popup(popup).add_to(marker)
    marker_cluster.add_child(marker)
for k in range(len(location2)):
    location = location2[k][0], location2[k][1]
    marker = f.Marker(location=location,icon=f.Icon(color='blue'))
    popup = 'lon:{}<br>lat:{}'.format(location[1], location[0])
    f.Popup(popup).add_to(marker)
    marker_cluster.add_child(marker)
marker_cluster.add_to(m)
m.save('OD_%s.html'%period)

使用MarkerCluster对于早高峰时段的聚类结果为：

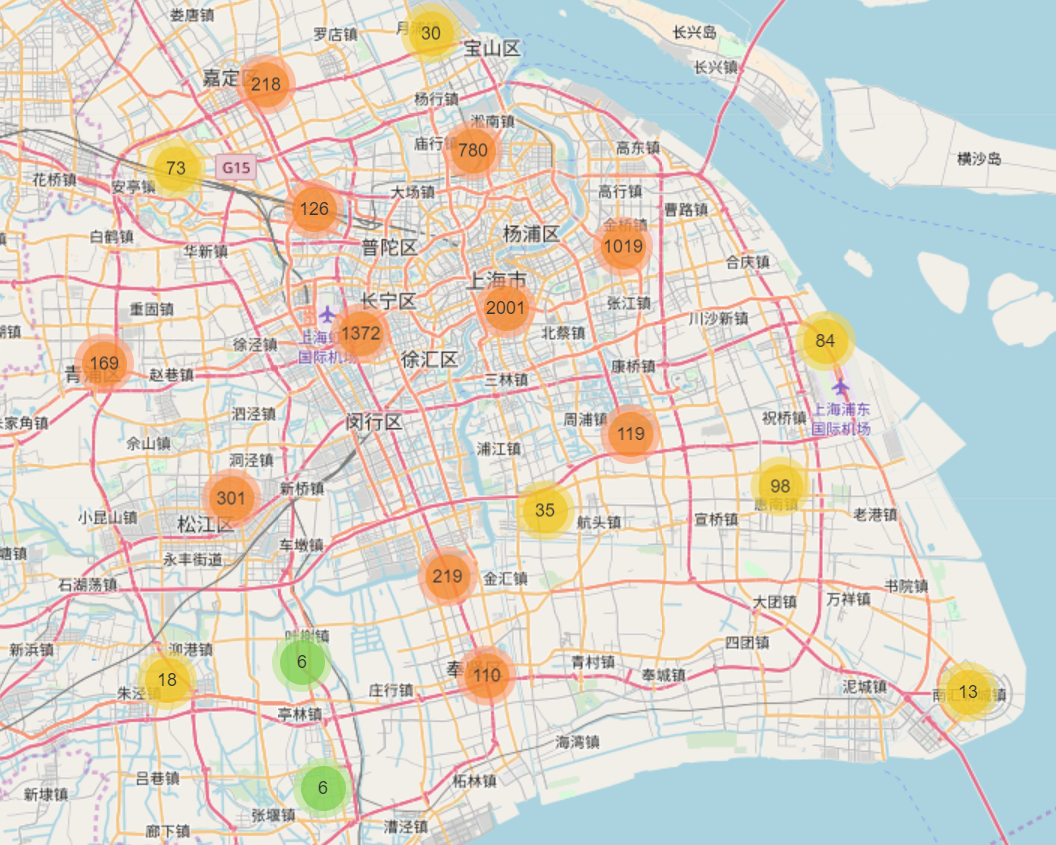
OD_morning

点击查看动态效果

对于晚高峰的聚类结果为：

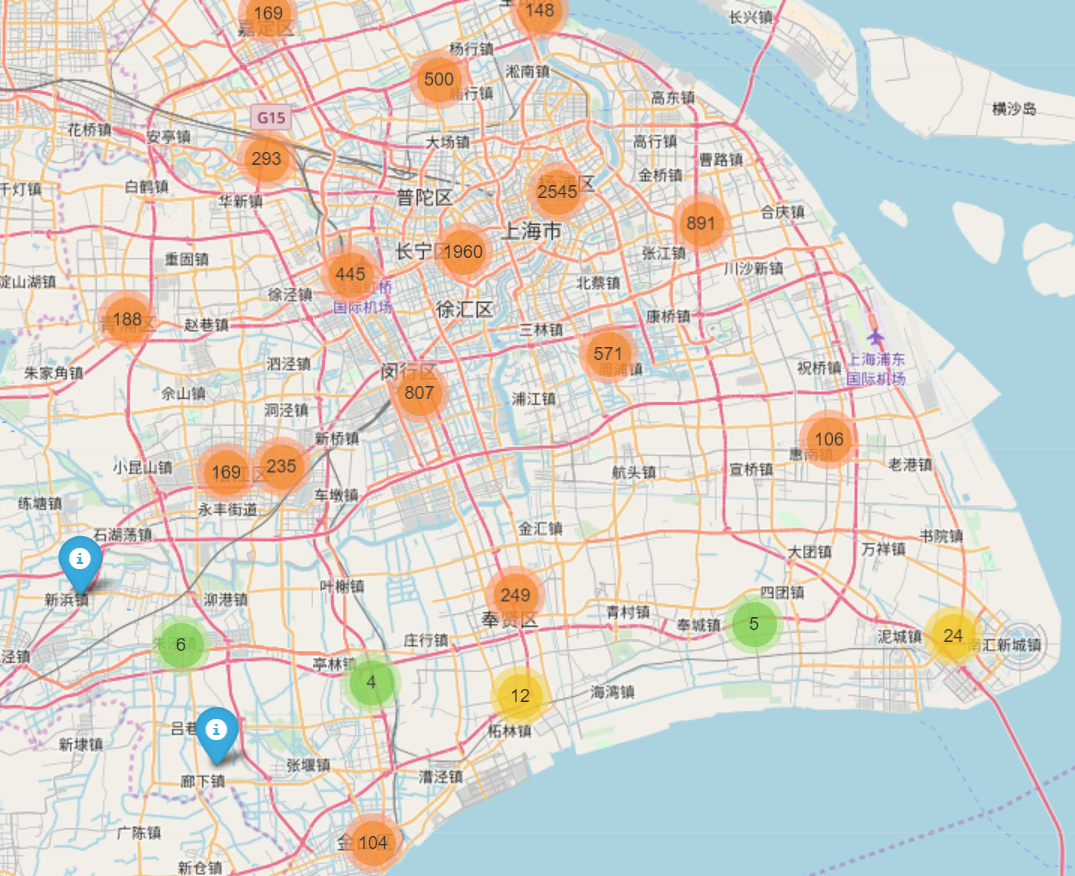
OD_night

点击查看动态效果

6.总结与分享

本次大作业与GIS的应用关系密切，虽然没有使用什么高级算法，但通过阅读各类博客、文献、网站，也使我对于回归、聚类算法有了新的认识，与此同时，我也掌握了很多利用Python进行gis分析的方法。

目前，我使用过的模块主要有geopandas、osmnx、networkx、folium，这些模块之间也有相互依赖与包含的关系。使用感受来看geopandas的功能十分强大，囊括了很多GIS分析方法；osmnx由伯克利大神Geoff boeing编写，对于路网十分友好，且在线获取地图的功能非常给力；networkx主要针对各类网络分析，理想化的网络也能处理，内置了我们常用的dijkstra,A*等算法；folium库主要与在线地图有着密切的联系，是绘制在线地图的良好方式。

回归补全数据、聚类还是进行交通分析的前期的步骤，接下来仍需结合数据显示的结果进行分析，因为是机器学习课程，涉及到的分析这里就不再详细叙述了，本篇也是在完成作业的基础上，记录一下整个数据处理流程，对于交通这类应用类学科，学会“掉包”、调效果好的“包”还是很重要的。很多事真正操作后才发现难度之所在，之前为本次作业设想的种种“宏图大志”到此也因为时间原因必须结束了，一路遇到各类想不到的bug，但感谢各种前辈的分享与大佬的解答，让我通过各种途径解决了问题。感谢！

最后，期末加油！

使用机器学习分析出租车订单数据

1. 问题背景

2. 出租车轨迹与订单数据

2.1 订单数据

2.2 轨迹数据

3. 数据预处理

3.1 导入模块、数据、查看异常数据

3.2 异常数据的筛选与结束时间的回归补全

Step1 计算通行时间

Step2 查看通行时间特点，删除异常数据

Step3 直线距离计算

Step4 查看直线距离特点，删除异常数据

Step5 回归分析直线距离与通行时间之间的关系

Step6 结合地理信息(路网)求算两点间的最短路网距离

Step7 回归分析路网最短距离与通行时间的关系并填充异常数据

4. 聚类分析

4.1 聚类方法选取

4.2 使用DBSCAN方法进行不同时段的OD点聚类

5. 利用MarkerCluster进行聚类与可视化

6.总结与分享