机器学习之主成分分析

发表于 | 分类于 | 浏览 次

PCA概述

高维数据劣势

我们很希望有足够多的特征（知识）来保证学习模型的训练效果，尤其在进行图像处理时，高维特征是在所难免的，但是，高维的特征也有几个如下劣势：

  1. 学习性能下降，知识越多，吸收知识（输入），并且精通知识（学习）的速度就越慢。

  2. 过多的特征难于分辨，你很难第一时间认识某个特征代表的意义。

  3. 特征冗余，如下图所示，厘米和英尺就是一对冗余特征，他们本身代表的意义是一样的，并且能够相互转换。

PS这篇实在是没有时间仔细来写了，就简单进行一下叙述，改日再续。。。

PCA的解释一

PCA，Principle Component Analysis，即主成分分析法，是特征降维的最常用手段。PCA 能从冗余特征中提取主要成分，在不太损失模型质量的情况下，提升了模型训练速度。

投影误差

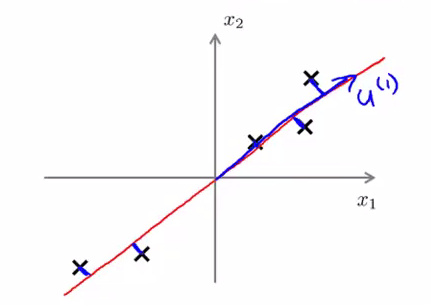
如上图所示，我们将样本到红色向量的距离称作是投影误差（Projection Error）。以二维投影到一维为例，PCA 就是要找寻一条直线，使得各个特征的投影误差足够小，这样才能尽可能的保留原特征具有的信息。

假设我们要将特征从 $n$ 维度降到$k $维：PCA 首先找寻 $k$ 个 $n$ 维向量，然后将特征投影到这些向量构成的$k$维空间，并保证投影误差足够小。下图中，为了将特征维度从三维降低到二位，PCA 就会先找寻两个三维向量

$u^{(1)}$,$u^{(2)}$二者构成了一个二维平面，然后将原来的三维特征投影到该二维平面上：

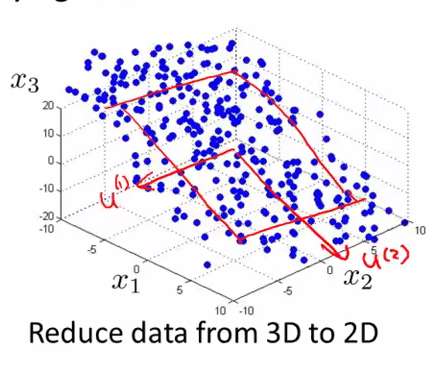
三维到二维

PCA的解释二

在PCA中，是一个坐标变换的过程，高维数据变到低维数据，数据从原来的坐标系转换到新的坐标系，那么坐标系应当如何选取呢？转换坐标系时，以方差最大的方向作为坐标轴方向，这里的方差最大指数据在该坐标轴的投影的值的方差，因为数据的最大方差给出了数据的最重要的信息。

​ 1.第一个新坐标轴选择的是原始数据中方差最大的方向，

​ 2.第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向

​ ……

​ 3.重复该过程，直至新坐标轴数量足够多。

通过这种方式获得的新的坐标系，大部分方差都包含在前面几个坐标轴中，后面的坐标轴所含的方差远小于前面的。于是，我们可以忽略余下的坐标轴，只保留前面的几个含有绝大部分方差的坐标轴。事实上，这样也就相当于只保留包含绝大部分方差的维度特征，而丢弃了包含方差小的特征维度，也就实现了对数据特征的降维处理。

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
###此段代码来源于《机器学习实战》，为pca.py文件
from numpy import *

def loadDataSet(fileName, delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [list(map(float,line) )for line in stringArr]
    return mat(datArr)

def pca(dataMat, topNfeat=9999999):
    meanVals = mean(dataMat, axis=0)
    meanRemoved = dataMat - meanVals #remove mean
    covMat = cov(meanRemoved, rowvar=0)
    eigVals,eigVects = linalg.eig(mat(covMat))
    eigValInd = argsort(eigVals)            #sort, sort goes smallest to largest
    eigValInd = eigValInd[:-(topNfeat+1):-1]  #cut off unwanted dimensions
    redEigVects = eigVects[:,eigValInd]       #reorganize eig vects largest to smallest
    lowDDataMat = meanRemoved * redEigVects#transform data into new dimensions
    reconMat = (lowDDataMat * redEigVects.T) + meanVals  
    return lowDDataMat, reconMat

def replaceNanWithMean(): 
    datMat = loadDataSet('secom.data', ' ')
    numFeat = shape(datMat)[1]
    for i in range(numFeat):
        meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) #values that are not NaN (a number)
        datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal  #set NaN values to mean
    return datMat
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
###此段代码测试文件main.py
from pca import *
from matplotlib import *
import matplotlib.pyplot as plt
import matplotlib.image as mpimg # mpimg 用于读取图片
import numpy as np

dataMat = loadDataSet("testSet.txt")  
lowDMat, reconMat = pca(dataMat, 1)  
shape(lowDMat)  #查看矩阵维数

fig = plt.figure()  
ax  = fig.add_subplot(111)  
ax.scatter(dataMat[:,0].flatten().A[0], dataMat[:,1].flatten().A[0], marker="^", s=90)
ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0], marker="o", s=50, c="red")  
plt.show()