机器学习之线性回归与局部加权线性回归

发表于 | 分类于 | 浏览 次

《机器学习实战》第8章 预测数值型数据：回归

不知道算是第几次接触、学习回归，如果没记错的话：大一的建模课、熊熊的数据采集处理、在弃坑Andrew Ng的网课前……一直到本次的自学。对于一些问题理解的不深刻是我一直以来的问题，这个问题主要源于我对线性代数内容的不熟悉，对理论的推导过程不熟悉等等因素。本学期机器学习课程又一次接触回归问题，希望这一次可以做一个比较完整的梳理，以备以后学习结束后及时复习、查看~

1
2
3
#本部分需要调用的库
from numpy import *
import matplotlib.pyplot as plt

内容提要：
线性回归
局部加权线性回归
预测鲍鱼年龄的实例

一、线性回归(LR)

1.线性回归含义解释

线性回归是给定一系列点数据点，建立“最佳“”近似“”线性“关系。回归的目的是预测数值型的目标值，回归的过程就是求回归方程的回归系数。

  • 最佳：有不同的定义；如：找出使误差（预测y值与真实y值之间的差值）最小的回归系数，这里的误差一般采用平方误差
  • 近似：由于模型误差与测量误差的存在，不能完美地描述数据
  • 线性：与线性代数存在一定关系

2.线性回归回归系数最优估计推导

线性回归估计w最优解的公式推导过程：

假定有线性方程：$Y=Xw$，找到最佳近似解$\hat{w}$，使平方误差$E(\hat{w})=(Y-Xw) ^ \mathrm{ T }(Y-Xw) $最小。

方法一：

展开该式：

此处补充线性代数转置常用的几个公式，因为真的每次都会忘：$(A^T)^T=A$; $(AB)^T=B^T A^T$; $(A\pm B)^T=A^T \pm B^T$ 。

由于$Y^\mathrm{T}Xw = w^\mathrm{T}X^\mathrm{T}Y$ 所以以上公式可以转换为：

令$K=X^TX$，$f=X^TY$，则以上变为：$E(\hat{w})=w^\mathrm{T}Kw - 2w^\mathrm{T}f + Y^\mathrm{T}Y$，此公式是一个二次型，因此由二次型的性质值当$K\hat{w}=f$时，$E(w)$取得最小值，将$K$与$f$带入，得到$X^T X \hat{w} = X^T Y$，若$(X^TX)^{-1}$存在，则有:

方法二：

直接将平方误差公式对w求导，得到$x^T(Y -X w)$，令其等于0，解得$\hat{w} = (X^TX)^{-1}(X^TY) $

使用以上两种方法的过程中都需要确定$X^T X$的逆矩阵是否存在。

在进行线性回归时通常有m个样本n个特征，则$Y=Xw$可以表示为下矩阵乘法。在这使用numpy计算的过程中需要注意数据的维度问题。

3.线性回归效果检验

计算预测值yHat与真实值y序列的匹配程度，匹配程度这一个量是通过两个序列的相关系数来体现出的。利用Python中的numpy模块，可以使用来进行计算：

1
np.corrcoef(yEstimate,yActual) #保证两个向量均为行向量，注意是否需要转置等操作

4.线性回归的程序实现

原始数据由三列组成，第一列为全1，第二列为x值，第三列为y值。数据读入过程为：

1
2
3
4
5
6
7
8
9
10
11
12
13
from numpy import *
def loadDataSet(fileName):      #读入Tab键分隔数据的一般函数
    numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields 
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat#此处读的y标签为行向量，后来部分场景需要转置操作

接下来为构建线性回归的函数：

1
2
3
4
5
6
7
8
def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0.0:
        print ("This matrix is singular, cannot do inverse")
        return
    ws = xTx.I * (xMat.T*yMat) #也可以写成ws=np.linalg.solve(xTx,xMat.T*yMatT)
    return ws

调用函数时即可采用以下步骤，并可以进一步绘图显示线性回归的效果。

1
2
3
4
5
>>> xArr,yArr = loadDataSet('文件名.txt')
>>> ws = standRegres(xArr, yArr)
>>> xMat = mat(xArr)
>>> yMat = mat(yArr)
>>> yHat = xMat*ws
1
2
3
4
5
6
7
8
9
10
#运行完以上参数后定义该函数，而后调用即可绘制回归曲线
def draw_picture(x,y,w):
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(x[:,1].flatten().A[0],y.T[:,0].flatten().A[0])
    xCopy = x.copy()
    xCopy.sort(0)
    yHat=xCopy*w
    ax.plot(xCopy[:,1],yHat,c='k')
>>> draw_picture(xMat,yMat,ws)

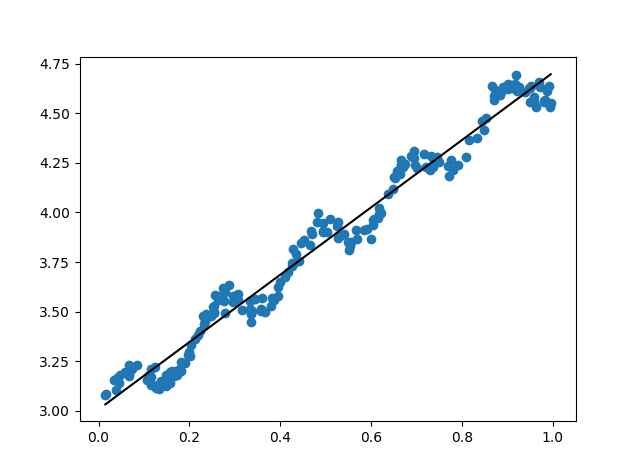
回归图像示例

二、局部加权线性回归(LWLR)

1.局部加权线性回归的含义解释及推导

在局部加权线性回归中，我们给待预测点附近的每一个点赋予一定的权重，对于赋予权重后计算最小均方差来找到较好的$\hat{w}$，从而进行进一步回归。即对于普通的线性回归来讲是找到$w$使$\sum_i(y^{(i)} - x^{(i)}w)^2$最小，但加权线性回归则是找到$w$使$\sum_ic^{(i)}(y^{(i)} - x^{(i)}w)^2$最小。

对比以上线性回归过程，引入权重矩阵$C$（用于给每个点赋予权重），则有$X^T C X \hat{w} = X^T C Y$，可得回归系数:

$C$即涉及到LWLR使用到的所谓“核”的概念，可以针对附近的点赋予更高的权重，核的类型有多重选择，比如选择高斯核权重为：$c^{(i)}=\exp\left( \frac{\left|x^{(i)}- x \right|}{-2k^2}\right)$

其中$c^{(i)}$仅为对角元素，点x与$x^{(i)}$相距越近，该权重越大；相距越远，该权重较小。

2.局部加权线性回归的特点分析

  • 优点：在一定程度上避免了欠拟合的问题、过拟合问题，但并不能完全避免
  • 缺点：算法的代价大，因为在对每个点做预测时，都使用了整个数据集

3.局部加权线性回归的程序实现

局部加权线性回归只要依靠lwlr()与lwlrTest()两个函数进行实现,lwlr()函数是取某一点利用局部加权线性回归，得到y的预估值。lwlrTest()函数是通过循环遍历数据集每一点，得到在局部加权线性回归的条件下每个点的预估值。将lwlrTest()的结果连成折线即是局部加权线性回归的结果。两个函数中可以对$k$值进行调节，将得到不同的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))
    for j in range(m):                      #next 2 lines create weights matrix
        diffMat = testPoint - xMat[j,:]     #
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print ("This matrix is singular, cannot do inverse")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws
1
2
3
4
5
6
def lwlrTest(testArr,xArr,yArr,k=1.0):  #loops over all the data points and applies lwlr to each one
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

局部加权线性回归算法可以通过比较估计值yHat与真实值y之间的误差，求算测试样本平方差之和，来比较不同k值下的性能。计算误差函数定义如下：

1
2
def rssError(yArr,yHatArr): #yArr(测试数据testArr) and yHatArr both need to be arrays
    return ((yArr-yHatArr)**2).sum()

在实际运用中，需将数据集进行划分，划分为训练集、测试集，分别用于训练和测试。

三、预测鲍鱼的年龄

使用了UCI数据集[abalone]http://archive.ics.uci.edu/ml/datasets/Abalone的200条数据，并做一定数据预处理，原始数据见《机器学习实战》原始代码包。数据集记录了鲍鱼的年龄，鲍鱼的年龄可以从鲍鱼壳的层数推算得到。

1
2
3
4
5
6
7
8
>>> abX, abY = loadDataSet('abalone.txt')
#局部加权线性回归
>>> yHat10 = lwlrTest(abX[100:199], abX[0:99], abY[0:99],10)
>>> rssError(abY[100:199], yHat10.T)
#线性回归
>>> ws = standRegres(abX[0:99], abY[0:99])
>>> yHat = mat(abX[100:199]) * ws
>>> rssError(abY[100:199], yHat.T.A)

改变局部加权线性函数的k值，能够比较局部加权线性回归与线性回归的效果。

参考内容

Peter Harrington《机器学习实战》第八章
Andrew Ng CS229课程讲义Note1

本章内容还涉及岭回归、lasso与逐步线性回归，之前都在不同的地方听说过这些方法，但还没有深入学习了解，但我对这一部分内容我还是很感兴趣的，希望接下来有时间补充这部分内容。

此外：我一直认为自己在自学过程中，对于理论的理解不够深入，特别是通过这学期的课程见识了很多茅数、茅信的大佬们，深感自己仍有很大差距，但不知道这种深度应该如何训练、提高。如果大家有什么好办法，欢迎大家与我交流~